One of the research problems that I am working on involves evaluation of a subjective rating system. I have been using information theory to try to identify objects where the evaluators agree well and objects where the evaluators do not agree well. I also am working on identifying objects that an individual rater does poorly. The method is to measure when the surprisal of the category that a rater selected is much lower than the entropy (the average surprisal across all raters).
Basic definitions
Here are some definitions. If you have a probability, p, then the surprisal is defined as
$-log_2(p)$
Logarithms relate numbers to powers, and base two logarithms relate numbers to powers of 2 (4, 8,16, 32, 64, etc.) as well as powers of 1/2 (1/4, 1/8, etc.). For probabilities, of course, powers of 1/2 are the only relevant powers since it is impossible to have a probability larger than 1.
If p=1/32, then the surprisal is 5, which corresponds to an event that is as surprising as getting five consecutive heads on the flip of a coin. If an event has zero probability, the surprisal is infinity. We need to tread with a bit of care around this fact.
If an event has probability 1, then the surprisal is zero. This is a quantification of the fact that an event that always occurs offers no surprise. As a probability approaches zero, the surprisal increases without bound. A probability of zero corresponds to an infinite suprisial
Now assume that $n$ raters are asked to provide a categorical rating to an object. There are $k$ possible categorical ratings.
Let $n_1, n_2, …, n_k$ be the number of raters who selected each of the particular categories and define
$p_j=n_j/n$
Then the entropy is defined as
$e=-\sum_{j=1}^k p_jlog_2(p_j)$
There are some technical adjustments to the formula if one or more of the probabilities are zero, but they are not worth mentioning here.
An alternate definition
There is an alternative way to compute entropy that will produce the same number. If you replaced each rater’s classification with the probability for that classification across all raters, then transform those probabilities into surprisals, then the entropy would be the average surprisal across all raters.
Here’s a simple example. A rating system has four possible choices, A, B, C, and D. Eight raters evaluate an object, and four classify it as A, two as B, and one each as C and D. The four probabilities are
$\begin{matrix}p_1=0.5\p_2=0.25\p_3=0.125\p_4=0.125\end{matrix}$
so the entropy would be calculated as
$e=-\sum_{j=1}^k p_jlog_2(p_j)$
$\ \ = -(0.5 log_2(0.5) + 0.25 log_2(0.25) + 0.125 log_2(0.125) + 0.125 log_2(0.125))$
$\ \ = 0.5(1) + 0.25(2) + 0.125(3) + 0.125(3)$
$\ \ = 1.75
If you look at the individual rating, replace them with probabilities and then calculate the surprisals, you get
$e = (4(1) + 2(2) + 1(3) +1(3))$
Now notice in this example that there is no perfect consensus choice. A is the most popular choice though, and the surprisals of the four raters who chose A is 1. The two raters who selected B didn’t do quite as well and their surprisal 2. The raters who selected C or D performed the worst, and their surprisals are 3.Now “worst” is a word that should be used carefully here. Perhaps the seventh rater was the only one who recognized the correct rating. But in many settings, there is no way to know what the correct rating is, and then you should consider not the correctness of the rating, but rather consider how close a rater comes to the consensus finding.
The point is that entropy is an average of the four suprisals of 1, the two surprisals of 2, a single surprisal of 3, and another surprisal of 3.
Comparing individual surprisals to the average surprisal
Comparing the individual surprisal to the average surprisal is also very important. The four raters who chose the first category are less surprising than average (-0.75=1-1.75). The two rates who chose the second category are just a touch more surprising than average (0.25=2-1.75). The rater who chose the third category is more of a surprise (1.25=3-1.75) as is the rater who chose the fourth category.
For some objects, the raters are able to come close to a perfect consensus. In these settings, a deviation from the most popular choice should be considered very extreme. On the other hand, for some objects raters may not be able to produce a strong consensus. Then a deviation from the most popular choice should be treated with some deference and understanding.
Consider a rating system where the first 7 of the 8 raters agreed on a single classification. The surprisal for the first seven raters is 0.19 and the surprisal for the last rater is 3. The average surprisal is 0.54, so the last rater’s deviation from the average surprisal is 2.46.
Contrast this with the above example where only half of the raters agreed on the most popular category. The surprisal of the last rater is only 1.25 units higher than the overall average surprisal.
For the above examples, the efforts to quantify the degree of agreement with the consensus may seem a bit silly. After all, you can just look at the data and offer an opinion about how well someone agreed with the consensus. But in applications where a large number of raters evaluate and classify a large number of objects, the ability to quantify becomes more important. It allows you to select those objects which a particular rater viewed quite differently than the consensus across all raters.
Example from sperm morphology assessment
In a sperm morphology assessment workshop, 39 raters were asked to classify 80 sperm images as either normal, borderline, or abnormal. For some images one or two raters did not provide a classification, which I treated as a fourth category.
Some images were relatively uncontroversial, with almost all raters providing the same classification. Others were more controversial and individual raters could not agree among themselves which classification was appropriate.
Example of good agreement
Here are some examples where a particular rater (#30) agreed closely with the consensus and where he/she did not.

This is obviously a good situation, with rater #30 agreeing with everyone else that the sperm image was abnormal.

Here’s another good situation, with rater #30 agreeing with more than 80% of the other raters that this image was normal.
Examples of acceptable agreement
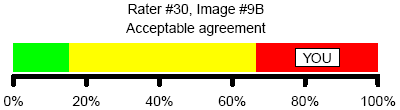
Here, the rater did not choose the most popular classification (borderline) but the abnormal classification still constituted a sufficient number of raters to allow this to be classified as acceptable agreement.
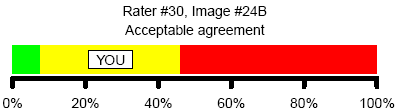
Here’s another example of acceptable agreement.
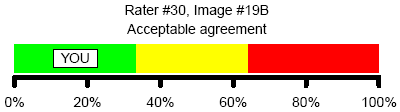
Here’s a sperm cell image where pretty much any choice should be considered acceptable because each choice garnered only 30-40% of the raters.
Examples of poor agreement
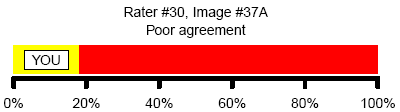
Here’s an example of poor agreement. Rater #30 chose a classification that was chosen by only 20% of the other raters.
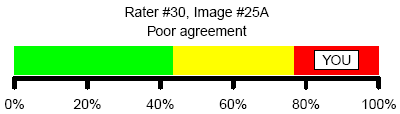
Here’s another example of poor agreement.
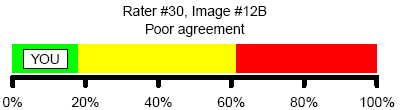
and another.
Examples of very poor agreement
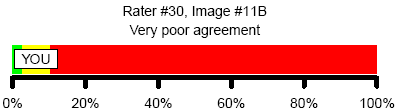
Here’s an example of very poor agreement: selecting a classification that only 10% of the other raters selected.
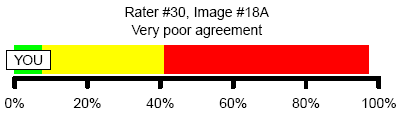
Here’s another example of a very poor agreement. The other raters are torn between two categories, but this particular rater did poorly by not choosing either of the two commonly selected categories.
Cautionary statement
Agreement with consensus is not necessarily the best choice. If there is an expert who can provide an accurate classification, you should compare your results to the expert.
You can find an earlier version of this page on my original website.