Suppose you compute a correlation coefficient from a sample of patients. Can you test a hypothesis about this correlation? Can you place confidence limits around this correlation? Yes, you can, but there are a wide array of approaches that you could use.
If you are testing the hypothesis that the correlation is equal to zero, you can compute a test statistic.
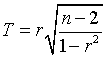
You would compare this test statistic with a t distribution with n-2 degrees of freedom. Someone asked me for a table of critical values for r. When the observed correlation is larger than the critical value, you would reject the null hypothesis. You can get the formula for the critical value:
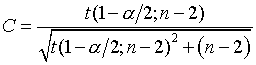
through simple algebra. I programmed a spreadsheet to perform these calculations.
If you want to compute a confidence interval for the correlation coefficient, you can’t necessarily assume that the population correlation is equal to zero. Instead, you use the Fisher’s Z transformation. I’ll write up some details about this transformation and work up some examples soon.
You can find an earlier version of this page on my old website.