I am updating some material about Poisson regression and noticed that some of the tests and confidence intervals rely on a percentile from a Chi-squared distribution or a gamma distribution. In previous work on binomial confidence intervals, I had noticed the use of a beta distribution and an F distribution. It seems odd to apply percentiles from continuous distributions for confidence intervals involving counting, but the formulas do indeed work. There are well known relationships for the cumulative distributions of the Poisson and binomial distributions that lead to these formulas.
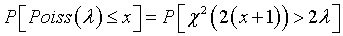
and
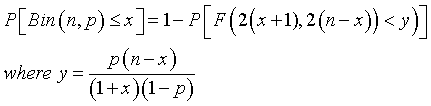
These can be found on page 127 and page 40, respectively of
Statistical Distributions Second Edition. Merran Evans, Nicholas Hastings, Brian Peacock (1993) New York: John Wiley & Sons. BookFinder4U link
The Wikipedia entries on the Poisson distribution and the binomial distribution refer to the incomplete gamma function and the regularized incomplete beta function, respectively, and this is, I suspect, another way of deriving the above relationships.
[Update: March 21, 2007] The relationship between the Poisson and the Chi-squared random variable is fairly easy to show if you recognize the relationship between the Chi-squared distribution and the Gamma distribution. The first equation above can be rewritten as
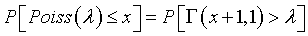
The left side of the equation equals
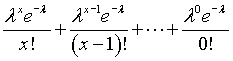
and the right side of the equation equals
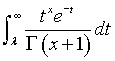
You can compute this by using integration by parts. If you let

then the integral simplifies to
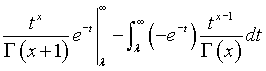
or
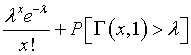
Repeat the process again to get
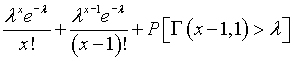
and again and again until you get down to

A gamma distribution with shape parameter 1 is simply an exponential distribution and this last probability works out directly to equal
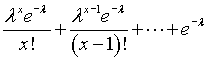
You can find an earlier version of this page on my old website.