suppressMessages(suppressWarnings(library(MASS)))
suppressMessages(suppressWarnings(library(tidyverse)))
knitr::opts_chunk$set(echo=TRUE, fig.width=8, fig.height=2)I want to write a paper about the hedging hyperprior. I need to work out some simple examples first. Here is an example involving the exponential distribution.
A simple Baysian analysis with an informative prior.
Consider a Bayesian analysis of an outcome variable that has an exponential distribution. The density of the exponential distribution is
\(f(x) = \theta^{-1} e^{-x / \theta}\)
You have an informative prior on \(\theta\) that has an inverse gamma distribution with prior parameters \(\alpha_0\) and \(\beta_0\).
\(g(\theta; \alpha_0, \beta_0) = \frac {\beta^\alpha_0} {\Gamma(\alpha_0)} \theta^{-\alpha_0-1} e^{-\beta_0 / \theta}\)
The mean of this prior distribution is
\(\frac{\beta}{\alpha_0-1}\)
You collect a sample of n data points, \(\mathbf{X} = X_1, X_2, ..., X_n\). This gives you a likelihood of
\(L(\mathbf{X}) = \prod_{i=1}^n f(X_i) = \theta^{-n} e^{-n \bar X / \theta}\)
and a posterior distribution of
\(h(\theta|\mathbf{X}) \propto \frac {\beta_0^{\alpha_0-1}} {\Gamma(\alpha_0)} \theta^{-\alpha_0-1} e^{-\beta_0 / \theta} \theta^{-n} e^{-n \bar X / \theta}\)
which simplifies to
\(h(\theta | \mathbf{X}) \propto \theta^{-\alpha_0-1-n} e^{-(\beta_0 + n\bar X) / \theta}\)
which, thanks to the miracle of conjugancy, is an inverse gamma distribution. With posterior paramaters
\(\alpha_1 = \alpha_0 + n\)
\(\beta_1 = \beta_0 + n\bar X\)
The posterior mean
\(\frac{\beta_0 + n\bar X}{\alpha_0-1+n}\)
can be written as a weighted average of the prior mean and the mean of the observed data.
\(\Big( \frac {\alpha_0-1} {\alpha_0-1+n}\Big) \frac {\beta_0} {\alpha-1} + \Big( \frac {n} {\alpha-1+n}\Big) \bar X\)
A simple numerical example
x_max <- 3
a0 <- 41
b0 <- 44
n <- 60
xbar <- 2.1
a1 <- a0 + n
b1 <- b0 + n*xbar
posterior_alpha <- a0+n
posterior_beta <- b0+n*xbar
x_grid <- seq(0.01, x_max, length=1000)
f <- function(x, theta) {
theta^(-1) *
exp(-x/theta)
}
g <- function(theta, alpha, beta) {
beta^alpha/gamma(alpha) *
theta^(-alpha-1) *
exp(-beta/theta)
}
prior05 <- 1/qgamma(c(0.975), a0, b0)
prior95 <- 1/qgamma(c(0.025), a0, b0)
post05 <- 1/qgamma(c(0.975), a1, b1)
post95 <- 1/qgamma(c(0.025), a1, b1) Let’s illustrate this with an informative prior with \(\alpha\) = 41 and \(\beta\) = 44.
g_grid <- g(x_grid, a0, b0)
outside <- x_grid < prior05 | x_grid > prior95
x_color <-
ifelse(outside, "white", "gray")
data.frame(x=x_grid, y=g_grid) %>%
ggplot(aes(x, y)) +
geom_segment(aes(xend=x, yend=0), color=x_color) +
geom_line() + xlab(" ") + ylab(" ")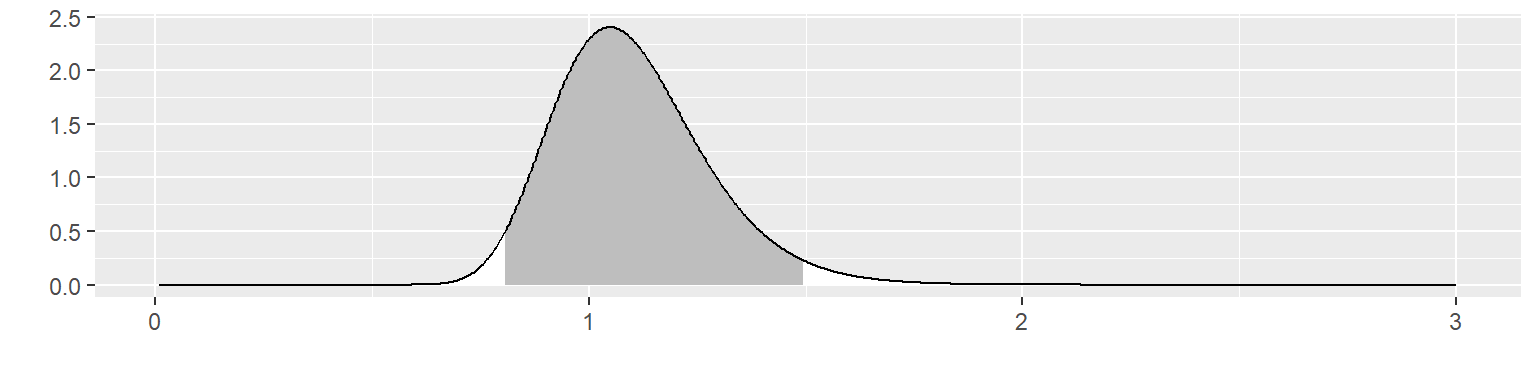
This corresponds to a fairly informative prior distribution. This distribution places \(\theta\) within 0.81 and 1.50 with 95% probability.
Let’s see what happens with this informative prior if you observe 60 values of x with a mean of 2.1. The likelihood is
f_grid <- f(xbar, x_grid)^n
x_color <- "white"
data.frame(x=x_grid, y=f_grid) %>%
ggplot(aes(x, y)) +
geom_line() + xlab(" ") + ylab(" ")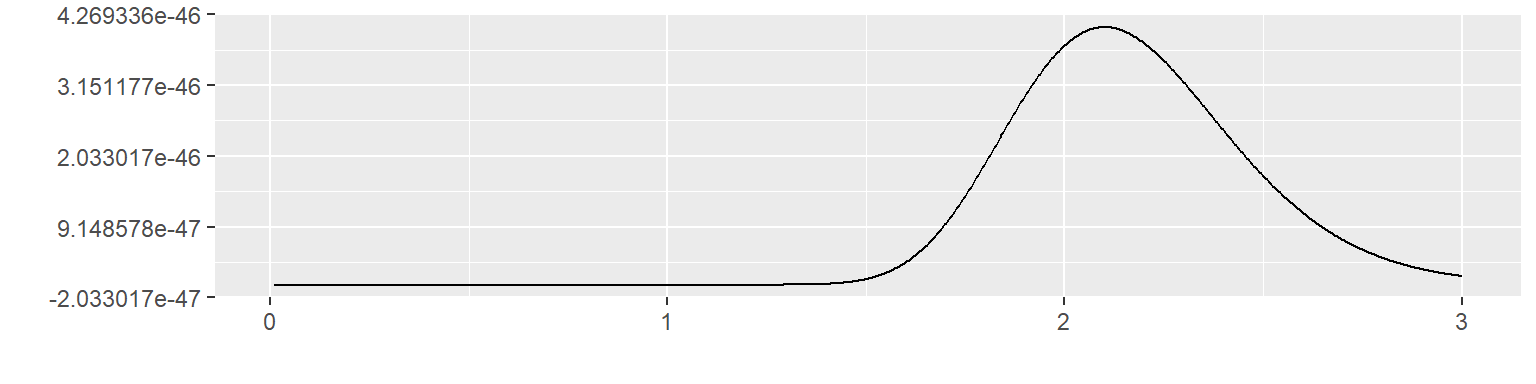
Multiply these two together to get the posterior distribution.
h_grid <- g(x_grid, a1, b1)
outside <- x_grid < post05 | x_grid > post95
x_color <-
ifelse(outside, "white", "gray")
data.frame(x=x_grid, y=h_grid) %>%
ggplot(aes(x, y)) +
geom_segment(aes(xend=x_grid, yend=0), color=x_color) +
geom_line() + xlab(" ") + ylab(" ")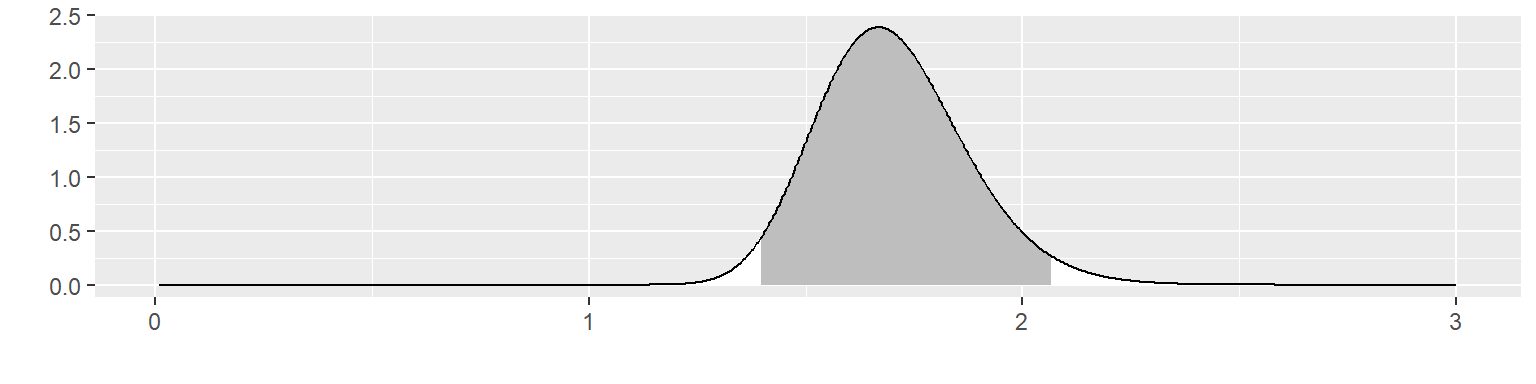
The posterior distribution is not close to either the prior distribution or the likelihood. It places \(\theta\) within 1.40 and 2.07 with 95% probability. It excludes the prior mean of 1.10 and it excludes 2.1, the mean of the data.
The hedging hyperprior
When the likelihood of your data and your informative prior are in conflict, you may wish to downweight the informative prior. You can do this by including a hedging hyperprior.
Define your prior distribution as an inverse gamma distributions with parameters \(1+\lambda (\alpha-1)\) and \(\lambda \beta\) where \(\lambda\) ranges between 0 and 1. Then place a hyperprior on the parameter \(\lambda\). The uniform(0,1) distribution is a reasonable choice for the hyperprior, but others are possible.
knitr::opts_chunk$set(echo=TRUE, fig.width=8, fig.height=8)lambda_grid <- seq(0, 1, length=60)
theta_grid <- seq(0, x_max, length=60)
gstar <- function(theta, lambda) {g(theta, lambda*(a0-1)+1, lambda*(b0-1)+1)}
density <- outer(theta_grid, lambda_grid, gstar)
op <- par(bg = "white")
z_max <- max(density, na.rm=TRUE)
persp(
theta_grid,
lambda_grid,
density,
zlim=c(0, 1.1*z_max),
xlab="theta",
ylab="lambda",
theta = 135,
phi = 30,
expand=0.5,
ticktype="detailed")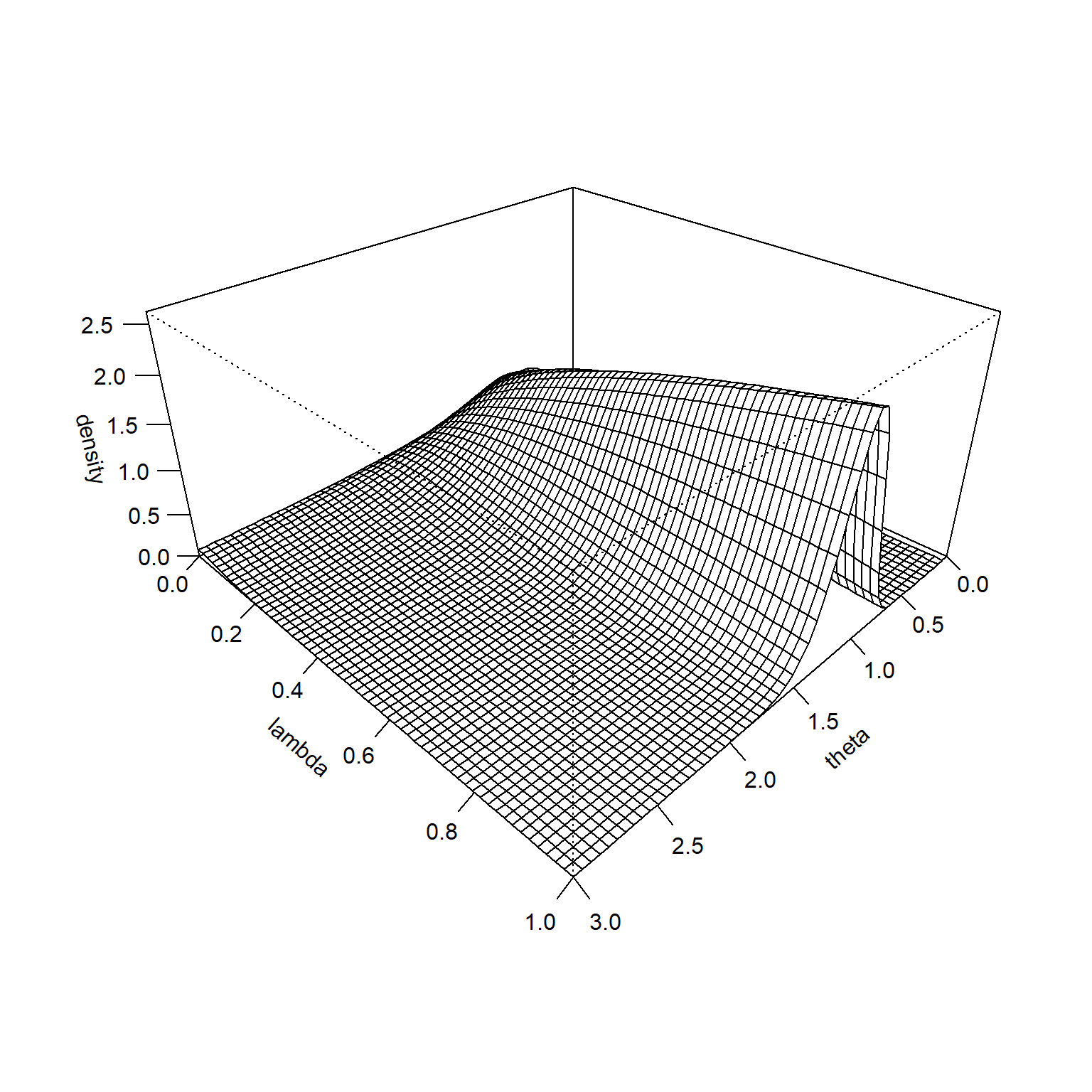
It is hard to see at this scale, but the prior distribution is higher for small values of \(\lambda\) when \(\theta\) is very large. This becomes more obvious if you remove the middle of the surface and rescale the Z-axis. There is a similar pattern on the far side of the graph. The prior trends towards a higher prior for small values of \(\lambda\) when \(\theta\) is very small.
This illustrates how the hedging hyperprior does its magic. It puts more probability on large values of \(\lambda\) (gives closer to full weight for the informative prior) when you observe data values close to the prior mean. It puts more probability on small values of \(\lambda\) (gives much less weight to the informative prior) when the data values are much larger or much smaller than the prior mean.
density <- outer(theta_grid, lambda_grid, gstar)
# density[12:32, ] <- NA
# density[11:40, ] <- NA
density[density>0.3] <- 0.3
op <- par(bg = "white")
z_max <- max(density, na.rm=TRUE)
persp(
theta_grid,
lambda_grid,
density,
zlim=c(0, 1.1*z_max),
xlab="theta",
ylab="lambda",
theta = 135,
phi = 30,
expand=0.5,
ticktype="detailed")
The likelihood function is constant across all values of \(\lambda\), so its surface looks like the following.
lambda_grid <- seq(0, 1, length=60)
theta_grid <- seq(0, x_max, length=60)
fstar <- function(theta, lambda) {f(xbar, theta)^n}
likelihood <- outer(theta_grid, lambda_grid, fstar)
z_max <- max(likelihood, na.rm=TRUE)
persp(
theta_grid,
lambda_grid,
likelihood,
zlim=c(0, 1.1*z_max),
xlab="theta",
ylab="lambda",
theta = 135,
phi = 30,
expand=0.5,
ticktype="detailed")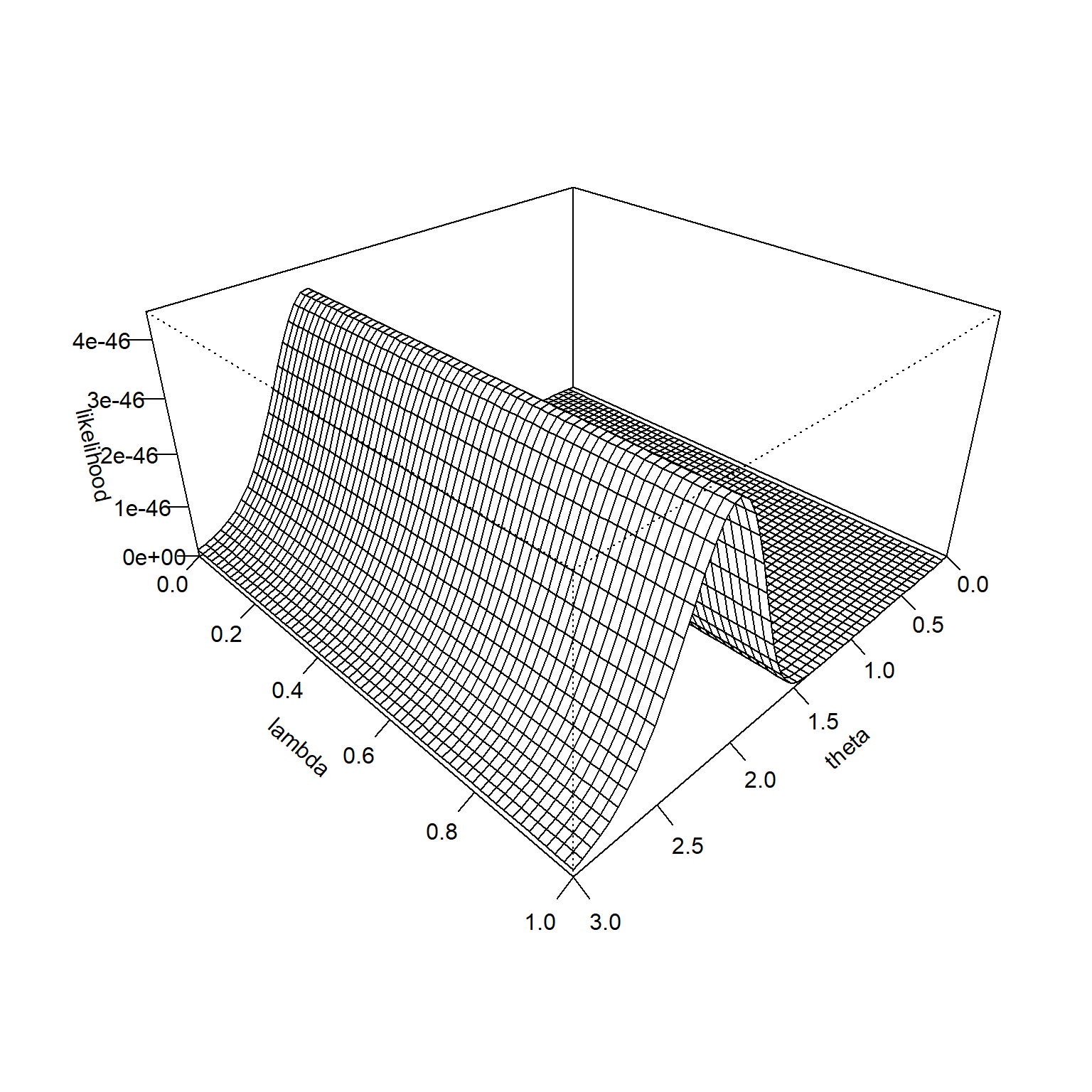
The product of the prior and the likelihood is proportional to the posterior distribution.
lambda_grid <- seq(0, 1, length=60)
theta_grid <- seq(0, x_max, length=60)
hstar <- function(theta, lambda) {g(theta, lambda*(a0-1)+1, lambda*(b0-1)+1)*f(xbar, theta)^n}
density <- outer(theta_grid, lambda_grid, hstar)
z_max <- max(density, na.rm=TRUE)
persp(
theta_grid,
lambda_grid,
density,
zlim=c(0, 1.1*z_max),
xlab="theta",
ylab="lambda",
theta = 135,
phi = 30,
expand=0.5,
ticktype="detailed")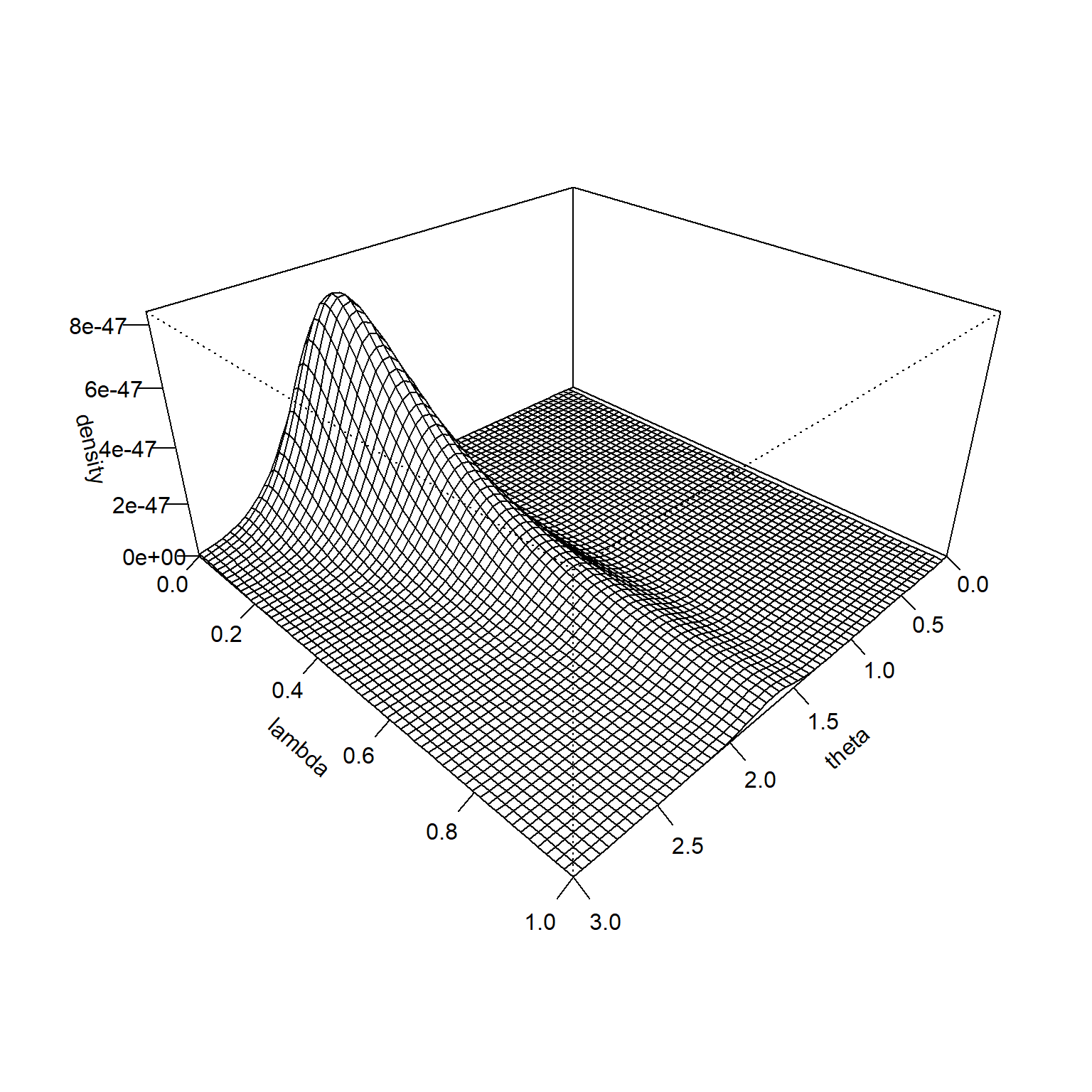
A contour plot shows where the probability is concentrated. The labels on the contour lines represent how much probabilty is found inside the contour line.
density <- density / sum(density, na.rm=TRUE)
density %>%
as.vector %>%
sort %>%
rev -> sorted_density
cumulative_p <- 0
for (p in sorted_density) {
cumulative_p <- p + cumulative_p
density[density==p] <- cumulative_p
}
contour(
theta_grid,
lambda_grid,
density,
labcex=1,
levels=c(10, 25, 50, 75, 90)/100,
xlab="theta",
ylab="lambda")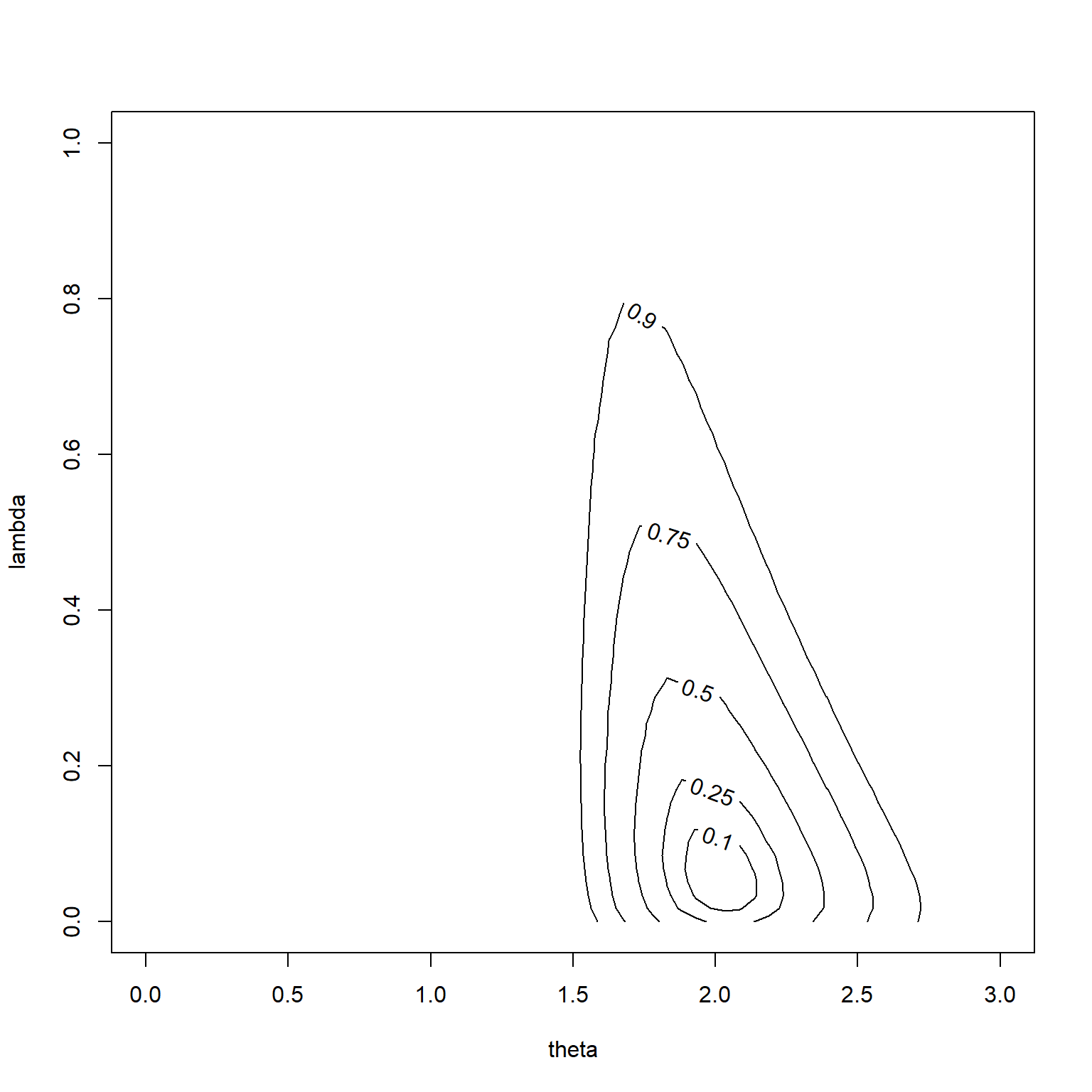
You can see that the hedging hyperprior did its job. The most probable values of \(\lambda\) are small and the prior mean (1.1) is largely ignored in favor of the mean of the data (2.1).