Dear Professor Mean,
How can we give an evidence based answer about why 20% loss of follow-up in a randomized trial is too much?
Dear reader,
This is a rule of thumb and you need to remember that no one ever got thrown in jail for violating a rule of thumb. There is a mathematical way of examining loss of follow-up rates that may prove useful. Let p represent the proportion of patients who are lost to follow-up. If you just ignored those patients, then you would have the following equation
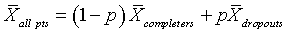
where the subscripts “all pts,” “completers,” and “dropouts” represent the mean response in all patients, patients who completed the study, and patients who dropped out. In a real research study, you would not know the mean for the dropouts, so you would not know how badly the mean of all patients differed from the mean of the completers. Even so, you will often have a subjective assessment on what the mean for the dropouts might be. This can help you get a rough idea of how dangerously you are living. You can rearrange the above equation using basic algebra to get
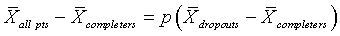
The left hand side looks like the relative error in using the mean of the completers in place of the mean of all patients, but the terms in the numerator are swapped and the denominator needs to be the mean for all patients, not the mean for completers. So you have to do a bit more algebra (which I find a bit tedious to do today), but the bottom line is that the relative error in using the mean of completers in place of the correct mean (the mean of all patients) is roughly proportional to the product of the proportion of dropouts and relative difference in the size of the outcome between dropouts and completers.
What does this mean? If the proportion of dropouts is small, that’s good news. If the difference in prognosis between dropouts and completers is small, that’s more good news. If both are small, you are truly worry free. If both are large, you’re in big trouble and you know it.
The tricky case is when only one is small. You should be okay as long as the other one isn’t horribly bad. So a small dropout rate is okay even with unequal prognosis between completers and dropouts as long as the inequality is not too extreme. Similarly, if the difference in prognosis is small, then any dropout rate that is not terribly extreme (less than 30% is what I’d say), should leave you in good shape.
Now it is possible to construct settings where a 10% dropout rate leads to disaster or where you’d be safe even with a 90% dropout rate, but these scenarios are unrealistic. My rule is don’t worry about a dropout rate less than 10% except in extraordinary settings. A dropout rate of 30% or higher though, is troublesome unless you have pretty good inside information that the difference in prognosis between dropouts and completers is trivially small.
It would be very difficult to come up with an evidence based justifcation of this rule of thumb. Such an effort would have to review studies where information on patients who dropped out somehow magically appeared. You could look at studies where dropouts were hunted down and hounded until they revealed what their response would have been, but this is troublesome on both pragmatic and ethical grounds. So I doubt that an evidence based answer could ever be obtained.
As an aside, the typical randomized trial has two arms (treatment and control) and dropouts are possible in either arm. The mathematics don’t change much, but it is worth noting that a dropout rate that differs between the treatment and control arms is almost always big trouble. A differential dropout rate could be caused by a variety of things, but it would hard to imagine a setting where a differential dropout rate between treatments and controls did not carry with it a large and unignorable degree of differential prognosis between completers and dropouts.
You can find an earlier version of this page on my original website.