In many situations, you need to generate a random sample from a distribution that is rather complex. When simpler methods for generating a random sample don’t work, there are a series of approaches based on the Markov chain principle that can help. There are several of these methods: Gibbs sampling, the Metropolis algorithm, the Metropolis-Hastings algorithm, that are collectively called Markov Chain Monte Carlo (MCMC). These approaches are especially valuable in Bayesian data analysis.
The simplest of the three methods is the Metropolis algorithm, and here is a simple example of how it works.
Suppose you have a distribution, where the density p is known, but where it is difficult or impossible to directly generate a random sample from that distribution. Typically p is a multivariate distribution, but in the example I show below, it is a univariate distribution.
Select a starting point X0 that satisfies p(X0)>0. At time points t=1, 2, …, sample a provisional value X*, not from p (which is difficult or impossible), but from a jumping distribution J(X*|X0). Notice that this is a conditional distribution, which means that the spot that you jump to depends on the value of X0. This jumping distribution has to have a symmetry property J(a|b)=J(b|a).
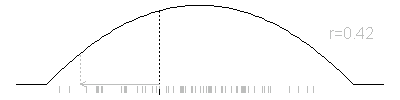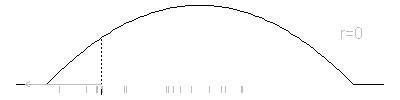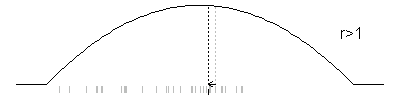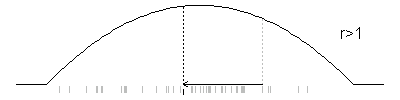
You will select a new value X1, which is either X* or X0. The selection depends on the ratio r=p(X*)/p(X0). If r is greater than 1, you always select X*. If r is less than 1, you select X* with probability r and X0 with probability 1-r.
Now repeat this process using X1. Select a provisional value X* from the jumping distribution J(X*|X1). Note that the jumping distribution is now conditional on a different value. Compute the ratio r=p(X*)/p(X1). Select X2 equal to either X1 or X* depending on the ratio r. Continue this process to generate X3, X4, etc.
The rationale for this approach is that you should look randomly in a variety of directions. If the new location is more likely than your current location, always sample the new location. If the new location is little less likely, then it makes sense most of the time to jump to the new location, but once in a while you will be better off staying at the current location. If the new location is much less likely, you will only rarely jump to that part of the distribution.
With any reasonable jumping function, you can show that this algorithm visits all the regions of the distribution and with probabilities that are appropriately large or small.
Here’s an example. The distribution function here has the form p(x)=6x(1-x) for 0<x<1, which is actually quite easy to simulate. But let’s see how the Metropolis algorithm would work for this situation. The jumping distribution I chose was normal with a mean equal to the previous iteration and a standard deviation of 0.2. At each iteration, I show the provisional value, but use gray if that value is not selected by the Metropolis algorithm.
To repeat this animation, press the REFRESH button on your browser.
The choice of jumping distribution is important. You don’t want the jumps to be too big or too small as either extreme can make the simulation process much less efficient.
Even with a good jumping distribution, this process is not as efficient as more direct methods of simulation. The Markov Chain property of this simulation introduces a positive correlation to successive values. This makes the set of values somewhat patchy unless the number of simulations is quite large. You would only use this approach if the more direct simulation methods were too difficult.
You can find an earlier version of this page on my old website.