The National Health and Nutrition Examination Survey (NHANES) is a large scale survey conducted by the Centers for Disease Control and Prevention (CDC). It uses a complex sampling scheme to insure that the results are representative of the population of the United States, excluding institutionalized persons. It is an unusal survey because it is combined with a physical exam, a dietary evaluation and a wide range of laboratory measurements from blood and urine samples. On this web page, I want to provide a not-too-technical overview of how CDC collects data for this survey as well as their recommendations on how to analyze it.
Introduction
The CDC provides a nice historical summary of NHANES. It started out as a series of surveys in the 1960s. the National Health Examination Survey. In 1971, the survey added information about nutrition and was re-labeled the National Health and Nutrition Examination Survey. The series of surveys were labelled NHANES I (1971 to 1975), NHANES II (1976 to 1980), NHANES III (1988 to 1994), and continuous NHANES (1999 to present). A closely related survey Hispanic Health and Nutrition Examination Survey (HHANES) focussed on three major Hispanic groups (Mexican Americans, Cuban Americans, and Puerto Ricans) and was conducted from 1982 to 1984. While various features of the sample and the data collected varied from one series to the next, the CDC made a conscious effort to maintain a broad similarity across these series to allow researchers to evaluate trends and changes over a multi-year period.
Although I will use NHANES as a generic description of all of the series of survey described above, the following descriptions will apply only to continuous NHANES. I also use the adjectives “small” or “large” throughout this document, and size always refers to number of people rather than square miles. So Cook Couny, Illinois with 5 million people, is a large county even though its area (1,600 square miles) is quite modest compared to other counties. And Nye County, Nevada, with 18,000 square miles would be described by me as a small county because only 46,000 people live there.
If you plan to analyze NHANES data, start at the main NHANES page of the CDC website and click on the Questionnaires, Datasets, and Related Documentation link. You might also find the link to tutorials helpful.
Complex survey
The first thing to recognize about the NHANES survey is that a simple random sample would be far too expensive to implement. If you wanted a simple random sample to be nationally representative, you would probably have to visit thousands of individual locations. The CDC saves an immense amount of money by sampling from clusters.
You can find a detailed description of the process at one of several sample design and estimation documents at the CDC website. I relied on the 2015 to 2018 document to prepare this summary. There are small differences in the cluster sample over time, but the process is largely similar for all years of the continuous NHANES survey.
There is clustering in done at four stages. The first level of clustering is at the county level, more or less. Counties with larger populations are divided into several pieces while counties with smaller populations are combined. These “counties” are labelled as Primary Sampling Units (PSUs).
These PSUs are assigned to different strata. These strata represent PSUs in a specific geographic area with certain features (e.g., small rural counties in the northeast). Two or more PSUs are sampled within strata. This, by itself is a great cost savings. There are about 3,000 counties in the United States, and you don’t want to be visiting that many different places.
PSU’s are sampled relative to their population size, with larger PSUs having a greater probability of selection. Some PSUs are so large that the probability of sampling them becomes 1. Others have sampling probabilities less than 1. The PSUs with sampling probabilities less than one are upweighted.
An overly simplistic explanation of why this is important is that PSUs with sampling probabilities less than 1 have to represent their peers that weren’t selected along with themselves. So, hypothetically, if you selected 2 PSUs out of a strata that had 20, you would have to upweight any estimates of those PSUs by 10 because each selected PSUs represents 10 PSUs (itself plus 9 unselected PSUs). This differential probability of sampling PSUs is the first reason you need to account for weights in NHANES.
The second stage of sampling occurs at the census block level. A census block is a small geographic region, sometimes as small as a single city block in big densely populated cities, but larger in less densely populated areas. Census blocks (or sometimes a collection of several census blocks) are randomly sampled within each selected PSU.
These census blocks are also selected relative to their population size and weighted accordingly.
A third stage of sampling occurs at the dwelling unit (DU). A DU could be a single family house, a duplex, or a multi-family apartment building. A random sample of DUs are selected within each selected city block.
The fourth and final stage of sampling occurs at the individual person level as a limited number of residents are selected randomly from each DU.
Oversampling
In order to insure accurate estimation, certain demographic groups are oversampled to insure that statistics on these groups have reasonable precision. The actual groups that are oversampled has varied over time. In the 2015-2018 cycle of NHANES, the oversampled groups included:
- Hispanic persons;
- Non-Hispanic black persons;
- Non-Hispanic, non-black Asian persons;
- Non-Hispanic white persons and persons of other racesand ethnicities at or below 185% of the federal poverty level; and
- Non-Hispanic white persons and persons of other races and ethnicities aged 0–11 years or 80 years and over.
When these oversampled groups are included in national averages, you need to downweight them so that they don’t skew the results. Oversampling is the second reason why you need to account for weights in NHANES.
Timing
Continuous NHANES runs in four year cycles. 60 PSUs are selected for each cycle and divided carefully into groups of 15 PSUs for each year. The selection insures that the 15 PSUs can produce nationally representative samples.
The publicly available NHANES data, however, is aggregated into two year intervals. The aggregation is done to help preserve privacy. Researchers who need to see year by year results must work at special Research Data Centers (RDCs) where access to the data is restricted to special computers to avoid disclosure of sensitive information.
If you are working with smaller demographic groups, you may need to aggregate across four years in order to get adequate precision.
Non-response
Participation in the NHANES survey is optional, so nonresponse is a problem. Nonresponse, at a minimum, reduces your precision. If different demographic groups have different nonresponse rates, you run the risk of losing the nationally representativeness of the survey.
The weights for individual patients are adjusted upwards in those demographic groups with high nonresponse rates to prevent these groups from being underrepresented in the overall sample.
Nonresponse is the third reason why you need to account for weights in NHANES.
Subsamples
NHANES includes multiple components (see below) and to save time and money, some of these components were administered to a subsample rather than the entire sample. As an example, only some of the participants aged 12 years and older were asked to provide blood samples for testing. There is an additional weight that you should incorporate to account for these subsamples.
This makes it a bit tricky, as you need to use different weights depending on whether you are using certain components of NHANES. If you are just using the interview data, the weighting variable is WTINT2YR. If, however, you use the tests of various metals in the blood sample, you need to use WTSH2YR as the weights.
Subsamples for certain components of NHANES are the fourth reason wy you need to account for weights.
Impact of the pandemic
Because of the COVID-19 pandemic, all data collection for NHANES was suspended in March 2020. This was a bit more than halfway through the planned 2019-2020 cycle. Although data collection was completed in 18 out of 30 Primary Sampling Units, these were not nationally representative. The partial data from this incomplete cycle was reweighted and combined with the previous two year cycle (2017-2018) to create the 2017-March 2020 pre-pandemic files.
Components
Questionnaire
Everyone in the NHANES sample gets a detailed questionnaire that asks about demographics and medical history of the participant and the participant’s family. Depending on a variety of factors, one, some, all, or none of the residents were selected to participate in the interview. Additional questionnaires are given during the medical examination.
Medical Examination
Some participants were asked to submit to a medical exam at a Mobile Exam Center (MEC), a series of mobile home trailers with various examination rooms. The physical exam takes about four hours.
A detailed dietary interview was also conducted at the MEC.
A subsample of those invited to the MEC were asked to provide biological specimens (blood, hair, nasal swab, oral rinse, urine, and vaginal swab). Details of the specimen collection process, including eligibility requirements, are available in an overview page.
A subsample of patients received an additional post-examination assessment.
Data analysis
CDC provides some general cautions about data analysis. More specific guidance is available in a web tutorial. The importance of using proper software to account for the complex survey design was repeatedly stressed.
Sample size issues
Group means and proportions between 0.25 and 0.75 should have a minimum sample size of 30. In addition, the effective sample size (sample size divided by the design effect) should also be at least 30. Any estimate with a relative standard error of 30% or greater should be explicitly identified as unreliable.
The criteria for proportions smaller than 0.25 or larger than 0.75 should require larger sample sizes, though the document does not explain this in any more detail. Alternative confidence intervals such as the Clopper-Pearson interval are also recommended for these proportions.
Population restrictions
If you wish to look at restrictions to your population (e.g., only children), you need to keep all of the data including adults and specify your restriction using a domain (subdomain, subpopulation) command.
In SAS, the domain is specified using the TABLES statement in PROC SURVEYFREQ and the DOMAIN statement in all other survey procedures.
Taylor series linearization
There are several approximations that are available in most data analysis software for estimating variances. The CDC recommends an approach, Taylor series linearization, for variance estimation. In SAS, you specify this using VARMETHOD=TAYLOR
Survey design variables
Information about the clustering and stratification also needs to be specified. In SAS, you need to account for these using the STRATA, CLUSTER, AND WEIGHT statements.
Data dictionaries
There are well over a thousand variables in the NHANES survey, so a good data dictionary is a must. There are several data dictionaries, actually, corresponding to multiple datasets. I list them here with a few key variables of interest to me.
-
Demographics: DEMO_I
- SDMVPSU, masked variance unit pseudo-PSU (used to designate clusters)
- SDMVSTRA, masked variance unit psuedo-stratum (used to designate strata)
- WTINT2YR, weight used for interview data
- WTMEC2YR, weight used for medical exam data
-
Dietary assessment, DR1IFF_I, DR2IFF_I, and others
- WTDRD1, weight used for dietary day 1 data
- WTDFD2, weight used for dietary day 2 data
-
Medical exam: AUX_I, AUXAR_I, and others
- You can find the weights for the medical exam data in the demographics file.
-
Laboratory data: AMDGYD_I, ALB_CR_I, and others
- WTSA2YR, Acrylamide and Glycimide weights
- WTSAF2YR, Apolipoprotein weights
- WTSA2YR, Aromatic diamines weights
- and so forth
-
Questionnaire data: ACQ_I, ALQ_I, and others
- Use one of the weights in the demographics file.
Note: these data are from the 2015-2016 survey. There are different data dictionaries for different times. Although many of the variables are the same, some are added or removed in different years. Some have different names or different number codes. So use caution when you combined data from multiple years.
Here’s an example of a cautionary statement about combining different
“Prior to 2011, one single question was used to collect information on language spoken at home for all non-Hispanic participants and the responses were released as variables ACD010A, ACD010B, and ACD010C. Starting 2011, to accommodate the Asian oversample, information on language spoken at home was collected separately for non-Hispanic Asians and other non-Hispanics using two different questions (i.e., ACQ110 and ACQ011). Analysts who wish to include “language spoken at home” data in analyses that use multiple 2-year NHANES cycles, may recode variables ACD011A, ACD011B, ACD011C, and ACD110 to create variables compatible with those released with the NHANES 1999-2010 data (i.e., ACD010A, ACD010B, and ACD010C) using the following SAS programming code:"
If SDDSRVYR in (7, 8, 9) then do;
ACD010B=ACD011B;
If ACD110 in (2, 3, 4, 5) then ACD010A=1;
Else ACD010A=ACD011A;
If ACD110 in (1, 2, 3, 4) then ACD010C=9;
Else ACD010C=ACD011C;
End;
Key demographic groups
Often with a survey like NHANES, you want to examine one or more subgroups rather than the entire population. Key demographic variables that you might want to use to create subgroups are found in DEMO_I and inclue
- RIAGENDR: Gender of the participant
- RIDAGEMN, the age at screening in months (for participants less than 24 months old)
- RIDAGEYR, the age at screening in years with 80+ year old coded as 80
- RIDEXAGM, the age at exam in months for participants less than 19 years old
- RIDRETH3: Race-ethnicity variable based on questions asked in 2011 and later. This differed from earlier surveys in the handling of Asian-American and Mexican-American responses.
- RIDRETH1: Race-ethnicity grouped using criteria before 2011
- DMDEDUC3: Highest level of education (participants ages 6-19 years)
- DEMDEDUC2 Highest level of education (participlants agess 20 years and above)
Example: blood lead levels in children in the 2015-2016 cycle
Here’s an example of the SAS code needed to estimate the average blood lead level in children under the age of six in the 2015-2016 cycle of NHANES.
Read the data
You will need to download two datasets:
You will need the complex survey variables: SDMVPSU and SDMVSTRA from DEMO_I and WTSH2YR from PBCD_I. To restrict the age range, you will need RIDEXAGM from DEMO_I. To get blood lead levels in ug/dL units, you will need LBXBPB from PBCD_I. Finally, you will need the SEQN variable in both datasets to merge them together properly.
NHANES stores their raw data in XPT format. This is a format developed by SAS, but the specification is open and other statistical packages should be able to read this format. You use the libname statement in SAS to read XPT files, and it takes a slightly non-standard format.
libname xp_demo xport "e:\git\nhanes\data\DEMO_I.xpt";
libname xp_pbcd xport "e:\git\nhanes\data\PBCD_I.xpt";
You should convert these two files into standard SAS files and store them in a separate folder.
libname mydata "e:\git\nhanes\perm";
data mydata.demo_i;
set xp_demo.demo_i;
run;
data mydata.pbcd_i;
set xp_pbcd.pbcd_i;
run;
Merge the data
Now merge the two datasets together by SEQN. At the same time, create a log transformed measure of lead and a variable to delineate subgroups for children 1-5 years of age. A common threshold used in lead studies is 5 ug/dl, so let’s also create an indicator variable for participants with blood lead levels above this threshold.
proc sort
data=mydata.demo_i;
by seqn;
run;
proc sort
data=mydata.pbcd_i;
by seqn;
run;
data mydata.merge2015;
merge mydata.demo_i(in=a) mydata.pbcd_i(in=b);
by seqn;
if (a) then in_demo=1; else in_demo=0;
if (b) then in_pbcd=1; else in_pbcd=0;
log_lead=log2(LBXBPB);
child1to5 =(RIDAGEYR>=1)&(RIDAGEYR<=5);
lead_ge_5=(LBXBPB>=5);
run;
The in_demo and in_pbcd variables will tell you how the two datasets match up. Every record in pbcd must also be found in demo, but the reverse will not be true. Here is the code to calculate how many records there are in each dataset and how they match up.
proc freq
data=mydata.merge2015;
tables in_demo in_pbcd;
title1 "Table of matches/mismatches";
run;
Calculate unweighted statistics
Don’t report the unweighted statistics, but it is a good idea to compute them just to get a feel for your data.
This is code to get unweighted statistics on the continuous variables of age and blood lead levels, and counts for the demographic subgroup variable.
proc means
n nmiss mean std min max
data=mydata.merge2015;
var RIDAGEYR LBXBPB;
title1 "Unweighted descriptive statistics";
run;
and unweighted counts on the demographic subgroup.
proc freq
data=mydata.merge2015;
tables child1to5;
title1 "Table of unweighted counts on demographic subgroups";
run;
It would be a good idea to do a few plots as well. You might draw histograms or look at boxplots, for example.
Get weighted counts and proportions
if you are interested in counts and proportions that are properly weighted, use proc surveyfreq,
proc surveyfreq
data=mydata.merge2015;
cluster sdmvpsu;
stratum sdmvstra;
table child1to5*lead_ge_5 / row nocellpercent;
weight wtsh2yr;
title1 "Weighted counts";
run;
You need to be sure to use the proper weights as noted above. For blood lead levels, the proper weights are in the variable wtsh2yr.
You also need to specify variables that identify the clustered nature of the survey (cluster sdmvpsu) and the stratified nature of the survey (stratum sdmvstra).
If you want to get statistics on a demographic subgroup, include that in the table statement. you do not want to create a smaller dataset with just that subgroup, because the smaller dataset will no longer have the information you need to process the data properly.
Here is the first part of the output.
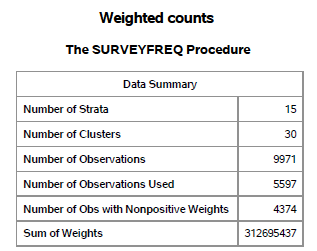
The data summary table confirms some of the frequency counts that we computed earlier. There are 9,971 unweighted observations in the dataset, but we can only use 5,597 of them because 4,374 have nonpositive (actually zero) weights. This is not surprising, because not every participant in the NHANES survey provided a blood draw.
The sum of the weights, 312,695,437 is the estimated population of the United States (excluding institutionalized people). The really important stuff comes in the second half of the output.
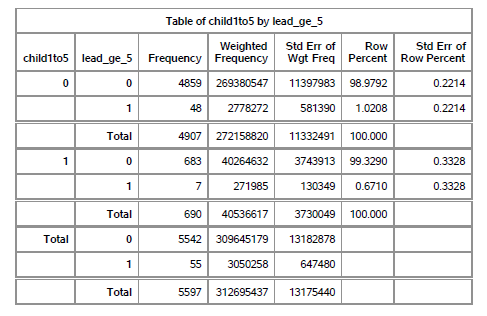
Focus your attention on row of the table where child1to5=1 and lead_ge_5=1. The frequency (unweighted count) is 7. This is a very small number, which is both disappointing and encouraging. If you look at the row beneath (child1to5=1, lead_ge_5=Total), you will see a frequency of 690.
So the survey got a blood tests done on a lot of children in the age range of 1 to 5, but only 7 of the actual tests run produced a blood lead value above 5 ug/dl. That bad news from a statistical perspective. Our estimate of the prevalence of elevated blood lead levels will be very imprecise. But from a public health perspective that’s good news.
Now the unweighted count is going to need adjustments for all the reasons noted above. The weighted frequency is 271,985. This means that there are roughly 300,000 children in the United States who had elevated blood lead levels in 2015-2016. Note that this is non-institutionalized children.
Also note how aggressively I rounded. The standard error (130,349) is very large relative to the mean. Any ration of the standard error to the weighted frequency of 0.3 or higher is troublesome. You could have guessed it from the small unweighted count but this is an additional confirmation that your estimate of this number is very imprecise. Put lots of warnings in your paper when you report this number. The number directly beneath 271,985 is the estimated total number of children with or without elevated blood lead levels in the United States. That number (40,536,617) is actually estimated with good precision. The unweighted count (690) is large and the standard error of the weighted count (3,730,049) is more than an order of magnitude smaller.
If there are 271.985 children 1 to 5 with elevated blood lead levels out of 40,536,617 total, the ratio is 0.6710 percent. During the time frame of 2015-2016, the probability that a 1-5 year old child in the United States has elevated blood lead levels is a bit less than 1%.
Note again the aggressive rounding. The standard error of this percentage, 0.3328 is large relative to the weighted percentage itself.
Get weighted means and standard errors
To get means and standard errors, use proc surveymeans.
proc surveymeans
data=mydata.merge2015
nobs mean stderr;
cluster sdmvpsu;
stratum sdmvstra;
var log_lead;
weight wtsh2yr;
domain child1to5;
title1 "Weighted means";
run;
The cluster, stratum, and weight statements use the same format as above. If you are interested in the means and standard errors for a particular demographic subgroup, include an indicator variable for that subgroup in the domain statement.
Here is a small but important part of the output from this procedure.
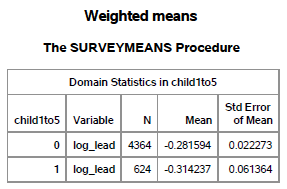
The second row of this table (child1to5=1) gives the average blood lead level on a log scale (-0.314237) and since this is on a base 2 log scale, you would calculate 2 raised to the -0.314237 power or 0.8042762. The average child in the United States aged 1 to 5 years has a blood lead level of 0.8 ug/dl. Since there are 624 unweighted participants who provided a measurable blood lead level, you can safely calculate a confidence interval.
On the log scale the confidence interval would be
$-0.314237 +/- 1.96 \times 0.061364$
or -0.4345104 to -0.1939636. Transform this back to the original scale to get 0.7399448 to 0.8742007.
We are 95% confident that the average blood lead level of all chidren aged 1 to 5 years in the United States is between 0.74 and 0.87.
References
Beilfuss, J., Camargo Jr, C.A., Kamycheva E. (2017). Serum 25-Hydroxyvitamin D Has a Modest Positive Association with Leukocyte Telomere Length in Middle-Aged US Adults. Journal of Nutrition. doi:10.3945/jn.116.244137.
Casagrande, S.S., Cowie, C.C. (2017). Trends in dietary intake among adults with type 2 diabetes: NHANES 1988-2012. Journal of Human Nutrition and Dietetics. doi:10.1111/jhn.12443.
Chang, T., Ravi, N., Plegue, M.A., Sonneville, K.R., Davis, M.M. (2016). Inadequate Hydration, BMI, and Obesity Among US Adults: NHANES 2009-2012. Annals of Family Medicine. 2016 Jul;14(4):320-4. doi:10.1370/afm.195.
Gabriel, A., Cohen, C.C., Sun, C. (2014). Consent to specimen storage and continuing studies by race and ethnicity: a large dataset analysis using the 2011-2012 National Health and Nutrition Examination Survey. Scientific World Journal. doi:10.1155/2014/120891.
Johnson, C.L., Dohrmann, S.M., Burt, V.L., Mohadjer, L.K. (2014). National Health and Nutrition Examination Survey: Sample design, 2011–2014. Vital and Health Statistics.