[StATS]: Randomization tests for paired data (January 24, 2006)
The randomization test offers a lot of flexibility for analyzing data in ways well beyond what traditional tests might offer. The concept is quite simple. Suppose that you ran a laboratory experiment, but a mischievous lab technician deliberately mislabeled some of your test tubes. What you would get would be properly described as “noise” and the results would be worthless. But in many situations, we are interested in how much noise there is in a data set and whether our signal readily exceeds the noise threshold. So you would deliberately shuffle the labels and analyze the data. Then reshuffle the labels and analyze again. Repeat this a few hundred or a few thousand times. Now compare the actual result from the unshuffled data to the results from the shuffled data. If the actual results lies smack dab in the middle of the shuffled results, then you are suspect that what you actually observed could have easily arisen from sampling error. If the actual result lies outside the shuffled results or very close to the edge of the shuffled results, then what you actually observed is unlikely to have appeared just by chance.
An interesting published example of the use of a randomization test appears in:
- Microsatellite diversity and the demographic history of modern humans. Jorde LB, Rogers AR, Bamshad M, Watkins WS, Krakowiak P, Sung S, Kere J, Harpending HC. Proc Natl Acad Sci U S A 1997: 94(7); 3100-3. [Medline]](http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&list_uids=9096352&dopt=Abstract) [Abstract]](http://www.pnas.org/cgi/content/abstract/94/7/3100) [Full text]](http://www.pnas.org/cgi/content/full/94/7/3100) [PDF]](http://www.pnas.org/cgi/reprint/94/7/3100.pdf)
Randomization tests should be used with caution, though, because you can only apply these tests properly when you understand how the data was collected. A good example involves the use of a randomization test with paired data. On this page, I want to illustrate how to do a randomization test properly when you have paired data and why an improper randomization test leads to a serious loss in precision.
Here’s a simple example from the Chance Data Sets web page. It represents weather predictions by five media outlets in Oklahoma City compared to the actual results. I will use a small subset of the data here, the one day forecasts from the fourth media outlet. Their predictions over a 338 day period were:
[1] 46 54 60 52 54 59 46 39 46 33 27 43 50 59 48 54 47 54 [19] 59 64 67 71 62 59 53 43 45 32 63 33 39 78 77 79 60 62 [37] 74 70 72 84 79 86 87 66 77 85 54 62 54 54 53 60 53 70 [55] 78 80 62 72 41 54 64 71 79 56 60 63 84 90 67 79 80 82 [73] 83 82 83 77 64 43 48 61 50 65 71 78 82 62 73 69 76 76 [91] 81 80 76 80 83 81 81 81 79 80 82 84 84 88 78 75 79 80 [109] 87 90 86 92 93 82 82 79 91 91 90 80 90 92 93 88 93 98 [127] 103 96 99 97 102 97 87 86 91 96 99 99 89 85 84 87 89 84 [145] 98 98 98 99 99 99 76 69 81 84 91 76 85 84 82 81 84 85 [163] 87 89 90 83 83 85 82 82 84 87 66 67 67 78 84 84 92 93 [181] 88 87 86 88 85 85 83 71 67 69 68 70 71 75 66 59 68 68 [199] 76 79 77 75 81 76 70 59 61 66 67 65 71 57 69 75 83 55 [217] 55 67 69 78 48 56 57 54 63 56 57 59 63 65 57 61 58 45 [235] 48 49 48 57 56 53 51 56 62 60 61 69 40 64 43 35 43 45 [253] 39 44 42 47 47 54 59 56 63 57 48 50 51 45 56 58 61 50 [271] 46 49 51 35 46 34 30 36 42 41 47 59 57 71 63 55 54 62 [289] 59 51 40 50 56 40 32 38 53 56 50 63 41 36 52 60 71 77 [307] 56 64 49 58 47 46 59 56 36 27 33 37 54 41 55 61 64 73 [325] 70 76 72 63 69 75 59 35 26 24 32 40 42 59
and the actual temperatures were:
[1] 50 46 48 48 52 54 50 40 34 35 29 45 50 46 51 48 46 52 [19] 61 58 61 68 67 56 62 48 43 38 60 50 44 74 74 68 56 53 [37] 77 74 72 82 75 81 75 70 80 80 68 59 59 51 54 56 53 73 [55] 79 65 65 72 54 49 67 67 69 72 68 57 79 81 62 79 86 87 [73] 79 82 87 77 69 58 56 70 60 65 72 84 87 69 74 74 75 82 [91] 80 80 79 86 87 83 83 81 81 83 84 86 86 86 78 77 85 87 [109] 85 93 93 93 94 85 87 87 91 93 94 93 91 93 93 92 92 94 [127] 99 95 99 95 97 97 88 92 94 95 97 96 88 87 86 88 88 88 [145] 96 95 99 98 98 97 87 75 79 85 90 86 84 85 87 88 88 90 [163] 90 89 88 83 82 81 83 83 86 86 69 58 59 72 83 83 83 91 [181] 92 89 84 84 83 82 83 73 64 73 71 70 73 71 72 67 71 75 [199] 72 73 79 79 78 74 73 62 63 71 77 65 61 66 68 78 74 70 [217] 63 71 73 72 58 60 63 66 64 61 55 57 63 59 61 54 60 51 [235] 55 59 56 66 60 50 48 57 67 62 68 71 40 38 49 40 40 43 [253] 42 45 48 45 41 54 58 54 58 55 51 50 58 54 54 54 56 49 [271] 48 48 41 38 43 33 29 32 38 41 56 56 60 66 55 52 56 61 [289] 57 52 42 54 53 41 36 44 56 47 55 56 44 37 46 58 64 69 [307] 56 56 48 55 50 47 50 53 27 28 48 60 54 42 54 67 64 71 [325] 72 73 65 65 72 67 71 46 30 31 36 50 53 60
There are several ways to measure the amount of agreement between a forecast and the actual value, and a simple thing to look for is whether the media outlet consistently overpredicted or underpredicted the actual temperature. There is perhaps some evidence for this. The mean estimate of the media outlet is 67.1 degrees and the average actual temperature across the same set of days is 66.4 degrees, a difference of 0.7 degrees.
The following graph shows the predictions across the 338 days with over predictions in red and under predictions in blue. Days where the prediction was perfect are represented by black dots.
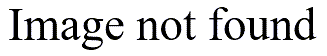
A simple, but incorrect, application of a randomization test would be to shuffle the labels so that of the 676 temperatures listed above, 338 would be randomly assigned to the media outlet and the other 338 would be assigned to the observed temperatures. The problem with this approach is that one sample might have a few too many winter values and the other sample might have a few too many summer values. It unnecessarily increases the variation in the randomization distribution.
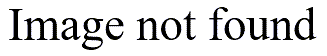
The picture shown above is what happens when you apply the randomization procedure incorrectly. Notice that some winter predictions were paired with summer observed temperatures and vice versa. While it probably does not affect the number of red or blue arrows, it certainly makes the deviations much larger than they should be. This leads to an unnecessary increase in imprecision and a subsequent loss of power.
To insure a proper mix of winter and summer days, a better approach is to randomly swap about half of the media outlet predictions with the actual values and to leave the rest unchanged. If the media outlet does not consistently underpredict or overpredict, then the observed difference of 0.7 degrees will fall well inside the distribution of differences in the randomization distribution.
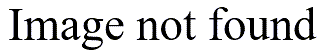
The picture above shows the better approach to randomization. It has a pattern that looks a lot like the original data, but if you look carefully, the colors (and hence the directions) of many of the arrows have switched. This is especially noticeable on the far right side of the graph, which was almost all red in the original graph, but which has a greater mix in the randomization distribution.
Here is the code for running a bad randomization that ignores the pairing in the data.
bad.distribution <- rep(-1,1000) for (i in 1:1000) { shuffle <- sample(c(media.outlet,observed.tmp)) media.outlet.bad.ran <- shuffle[1:338] observed.tmp.bad.ran <- shuffle[339:676] bad.distribution[i] <- mean(media.outlet.bad.ran)-mean(observed.tmp.bad.ran) }
Notice the approach: put both sets of data together and shuffle them in a random order (using the sample function). Then pick the first 338 values for the media.outlet randomizaiton sample and place the remainder in observed.temperature.
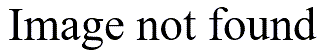
The results of this randomization appear above. Notice that the observed difference (0.7 degrees) falls well inside the randomization distribution. It turns out that 287 of the values in the bad randomization distribution are larger than 0.7, which would produce a p-value of 0.564 (you would take 287/1000, but then you have to double the p-value because it is a two sided test).
The code for using the pairing information in the randomization process is just a bit more complex.
good.distribution <- rep(-1,1000) for (i in 1:1000) { swap <- (runif(338) > 0.5) media.outlet.good.ran <- rep(-1,338) observed.tmp.good.ran <- rep(-1,338) media.outlet.good.ran[!swap] <- media.outlet[!swap] media.outlet.good.ran[swap] <- observed.tmp[swap] observed.tmp.good.ran[!swap] <- observed.tmp[!swap] observed.tmp.good.ran[swap] <- media.outlet[swap] good.distribution[i] <- mean(media.outlet.good.ran)-mean(observed.tmp.good.ran) }
First you create a swap vector that is true about half of the time. Then populate the media.outlet randomization scores with media.outlet values if you do not swap, and with observed.tmp values if you do swap. Reverse this for the observed.tmp values.
The distribution of values using the good randomization approach appears above. This distribution is much more precise because it does not mix summer predictions with winter observed values. Only 5 values in this distribution are larger than 0.7, producing a p-value of 0.01.
This general concept can be extended to more complex research designs. Many research designs have blocking factors, and the trick to performing a randomization test is to randomly shuffle within the blocks when you are testing an effect within blocks. For an effect between blocks you would just randomly shuffle the entire block.
Further reading in the StATS pages:
Further reading outside:
- Randomization Test on Means of Matched Pairs. Howell DC, The University of Vermont. Accessed on 2006-01-26. [Excerpt] In some ways the randomization test on the means of two matched samples is even simpler than the corresponding test on independent samples. From the parametric t test on matched samples, you should recall that we are concerned primarily with the set of difference scores. If the null hypothesis is true, we would expect a mean of difference scores to be 0.0. We run our t test by asking if the obtained mean difference is significantly greater than 0.0. For a randomization test we think of the data just a little differently. If the experimental treatment has no effect on performance, then the Before score is just as likely to be larger than the After score as it is to be smaller. In other words, if the null hypothesis is true, a permutation within any pair of scores is as likely as the reverse. That simple idea forms the basis of our test. www.uvm.edu/~dhowell/StatPages/Resampling/RandomMatchedSample/RandomMatchedSample.html
This page was written by Steve Simon while working at Children’s Mercy Hospital. Although I do not hold the copyright for this material, I am reproducing it here as a service, as it is no longer available on the Children’s Mercy Hospital website. Need more information? I have a page with general help resources. You can also browse for pages similar to this one at Category: Unusual data.
data](../category/UnusualData.html). for pages similar to this one at [Category: Unusual with general help resources. You can also browse Children’s Mercy Hospital website. Need more information? I have a page reproducing it here as a service, as it is no longer available on the Hospital. Although I do not hold the copyright for this material, I am This page was written by Steve Simon while working at Children’s Mercy