Someone wrote asking me about a variation of the “Rule of Three”. This rule says that if you observe zero events out of n, an upper 95% confidence limit for n is approximately 3/n. So suppose you operated on 10 patients and none of them died after surgery. Then you would be 95% confident that the mortality rate would be 30% (3/10) or less. This person asked “Suppose I repeatedly sample from a population and every patient in the sample was a G. What is the how likely is it that the entire population is Gs?” This flips the problem around, and is equivalent to saying that the probability of survival is 97% or greater. But this person wanted an estimate of the probability that the probability in the population is 1.
This is a question that is Bayesian. If you believe in classical statistics, the probability that the population contains only Gs is either zero or one. There is nothing random in a population, so you can’t assign any meaningful probability statements to the population.
If you are a Bayesian, then this sort of thing doesn’t bother you. You have a parameter, pi, and you place a prior distribution on pi. Collect some data and then combine it with the prior using Bayes rule to get a posterior distribution. How would this work in practice?
Well, the classic example is to put a beta prior on the binomial distribution. Often this is a flat or uniform prior, which is a beta(1,1). Here’s what the prior looks like.
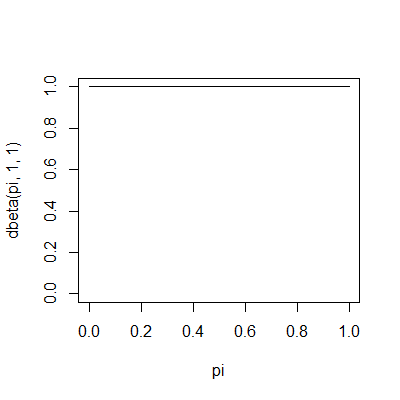
And now suppose that you observe 10 values from the sample and they are all Gs. The posterior distribution is now beta(11,1), which looks like this.
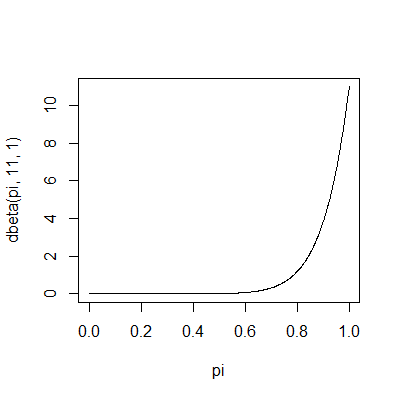
Most of the probability is concentrated above 0.7, which makes sense.
The problem with the beta prior distribution, though, is that it does not assign a non-zero probability to the probability of 0 or 1 or any other value. Let’s change the prior slightly. There are N items in the population and let’s assign a discrete uniform probability to the values 0, 1/n, 2/n, …, 1. Here’s what this looks like for N=100.
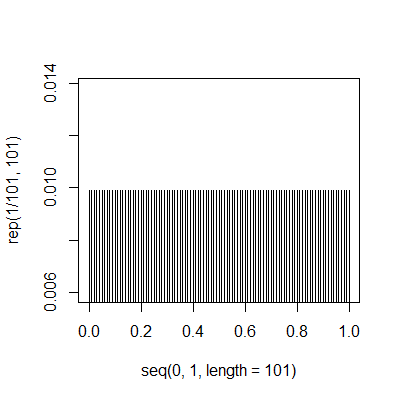
Now, suppose that you observe 10 patients in this sample and they are all Gs. The posterior distribution would look something like this.
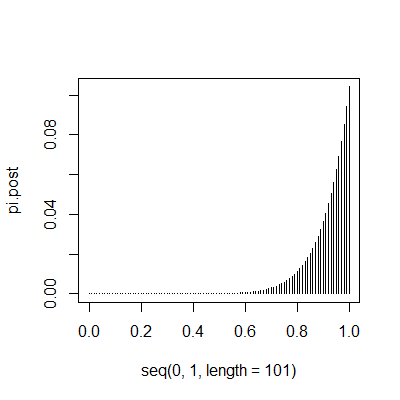
The probability that pi equals one is roughly 10%. When I get a chance, I will show the math for this example, and maybe the R code.
You can find an earlier version of this page on my blog.