This page is currently being updated from the earlier version of my website. Sorry that it is not yet fully available.
Someone sent me an email asking about the work that Byron Gajewski and I have done on monitoring accrual patterns in clinical trials. She had been doing something similar at her job and wanted to see if we could collaborate.
In her situation, the major issue was
- the number of patients who made an initial contact but did not keep their first appointment,
- the number of patients who kept the appointment, but refused to sign the consent form once they realized what the study was about, and
- the number of patients who did sign the consent form, but who did not meet the inclusion criteria once the initial screening was done.
Her data is interesting because her company recruits to multiple centers. The accrual pattern is also interesting, because in her job, she sees a sudden burst of recruits once an ad is placed, this will settle down and then another burst will occur when another ad is placed.
The loss of subjects during the course of recruitment is quite severe. Only one in every 20 patients makes it from the initial contact through all of the steps to final enrolment and randomization in the study. Such a large loss is probably unavoidable, because you can’t bypass the consent process and you can’t let just anyone into these studies. But clearly this loss has tremendous economic implications and we need to carefully plan for these losses and monitor them during the course of the study.
The geometric distribution provides an excellent approach to model the losses of patients prior to enrollment. The geometric distribution can be characterized as the number of independent Bernoulli trials observed until the first success. The probability mass function of the geometric distribution is
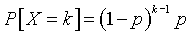
for k=1, 2, 3, . . .
Assume that there are k stages to the screening process from initial contact to final enrollment. At the initial planning stage for a study, we would ask the researcher to estimate the rejection/refusal rate at each stage, R~i~ or alternately the rate of success at each stage, S~i~. Of course
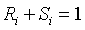
Let N~k~ represent the desired number of patients enrolled. The number needed at the initial contact would be
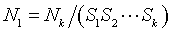
This presumes, of course, that our estimates of each rate is perfectly accurate. There are some advantages to using a Bayesian approach, so we would also solicit a prior distribution on each rate. The simplest prior distribution is a beta distribution. The actual process of soliciting a prior distribution is a topic for another time. Let us suppose that the prior distribution is
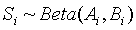
After n1 patients have been recruited into the trial, with s1 successes and r1 rejections/refusals at the first stage, s2 successes and r2 refusals at the second stage, etc., we would have a posterior distribution
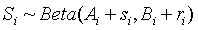
The expected value of the posterior distribution is
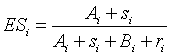
which can be written as a weighted average
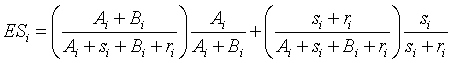
You can also simulate the number of initial contacts needed to enroll patients N~k~ by randomly drawing values from the posterior distributions and calculating sums of geometric distributions.
Example: This example is based on retrospective data, but will be treated as if the planning was done prospectively. A clinical trial needs to enroll 414 patients. The researcher notes that there are three stages at which rejection or refusal could occur.
- Stage 1: A volunteer could makes an initial contact, but does not set up a first appointment, cancels the first appointment, or fails to show up at the first appointment.
- Stage 2: At the initial appointment, the volunteer reviews the details of the study and does not want to join the study.
- Stage 3: After the consent form is signed, the volunteer gets some medical tests done. These tests show that the patient is ineligible for the trial.
The researcher estimates the probability of success at each of the three stages to be 20%, 90%, and 50%. The overall rate of success (surviving all three stages) is simply the product of these three probabilities (9%). This is a very small number, but represents the realities of conducting clinical trials. We cannot coerce people to join these trials, and it may be dangerous to set too broad an inclusion criteria. The time that the trial will take clearly is critically dependent on these values and even small declines in the success probabilities could produce major delays. It, therefore, becomes critical to plan these values carefully and to monitor them closely.
Since this is retrospective data, the success probabilities were deliberately chosen to be inaccurate. The actual success probabilities at the end of the study were quite different. It took 8,138 initial contact to get 2,449 volunteers to show up at the initial appointment (30% success rate). There were 2,084 who signed the consent form (85% success rate). Only 414 of these met the inclusion criteria (20%). Two of the initial estimates are too high and one is too low, but overall the projection is unduly optimistic because the overall success rate is 5%, much lower than the prior estimate of 9%.
A Bayesian model for these rates provides some valuable insights, and it is worth some effort to try to elicit an informative prior. Clearly the researchers on this project are not total novices and can offer some insights about their degree of certainty about their initial estimates of the success probabilities.
The process of eliciting an informative prior is very important but it is also very complex. I will defer discussion of this and place it in a separate web page. For now, assume that this process produces three beta distributions: Beta(A1=10,B1=40), Beta(A2=45,B2=5), and Beta(A3=25,B3=25). With these prior distributions, you can simulate how the trial will behave.
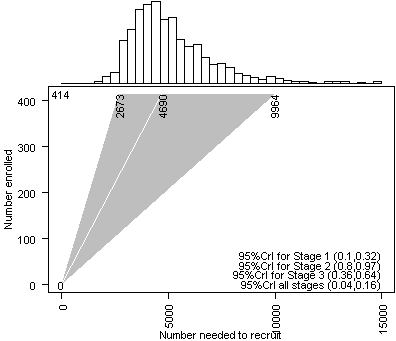
The graph shown above represents a simulation using 1000 replications. The median number of patients needed at the initial stage in order to get 414 volunteers who are willing and able to enrol in the study is 4,690. There is substantial uncertainty. There is a 2.5% probabilities that it could be 2,673 or smaller and a 2.5% probability that it could be 9,964 or larger. The histogram at the top of the graph shows the actual distribution of these values. The prior distributions represent the degree of uncertainty about the initial estimates and 95% credible intervals (CrI) are one way of displaying this uncertainty. The 95%CrI for the success probability at stage 1 (20%) ranges from 10% to 32%. At stage 2 (90% success probability), the interval is 80% to 97%. At stage 3 (50% success probability), the interval is 36% to 64%. The overall success rate (9%) has an interval from 4% to 16%.
The median projection of 4,690 falls far short of what actually happened in this clinical trial, of course, because the initial success probabilities were in general too optimistic. The Bayesian model will provide revised estimates of this projection as data accumulates during the trial.
This trial started very rapidly and after seven days, the 18 patients were enrolled in the study. There were some losses along the way to get these 18 patients into the trial. 61 volunteers did not meet the inclusion criteria (18/79 or 23% success at stage 3). 14 patients did not sign a consent form (79/93 or 85% success at stage 2). 222 did not make or keep their initial appointment (93/315 or 30% success at stage 1). The overall success rate (18/315 or 6%) is much lower than 9%.
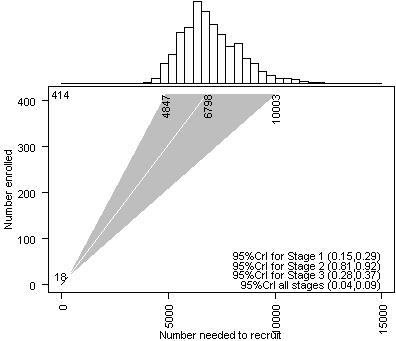
The graph above shows the Bayesian simulation combining the prior estimates with the observed data. Notice that the 95% CrI for Stage 3 has declined markedly as has the interval for the overall success rate. The interval for Stage 1 has increased. The projection for total number of patients needed to recruit initially to insure that 414 enroll in the trial is also much higher (though still short of the 8,139 observed at the end of the trial).
After 14 days, things have heated up even more. There are now 93 patients enrolled in the trial, though there were 340 lost at stage 3 (93/433 or 21% success rate), 66 lost at stage 2 (433/499 or 87% success rate), and 1070 lost at stage 1 (499/1569 or 32% success rate). The overall success rate (93/1569 or 6%) is about the same as before and still much lower than the initial estimate.
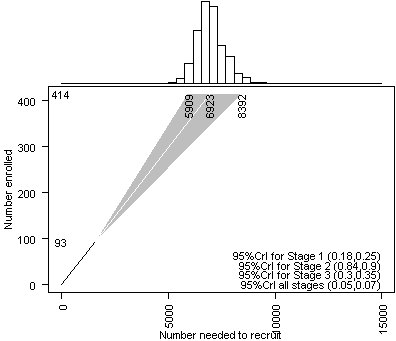
The graph above shows the Bayesian model incorporating the prior distributions and the 14 days worth of data. The number of initial contacts is now estimated to be 6,923 and the 95% CrI (5,909 to 8,392) is now much narrower, leading to more confident predictions.
Here is the code that produced these graphs.
projected.number.to.recruit <- function(nk,A,B,s,r, sim.size=1000,n0.max=2*nk/prod(A/(A+B))) { # nk is the desired number of patients who survive # all the rejection/refusal steps to get into the study. # A and B are the parameters of the prior beta # distribution(s). If more than one rejection/refusal # process is being monitored then A and B are vectors. # You can conceptualize A as a prior number of successes # and B as a prior number of failures (rejections/refusals). # s and r are the observed number of successes and failures # (rejections/refusals). Again, if more than one process # is being monitored, then r and s are vectors. # The output of this function will be a vector of # simulated values for n0, the number needed at the initial # stage to guarantee nk participant at the final stage. # The output also include p0, the overall success rate # across all k stages. k <- length(A) # If A, B, s, and r all do not have the same length, # the results of this function will be unpredictable. # When I get the chance, I want to check for this # before proceeding. n0 <- rep(NA,sim.size) p0 <- rep(1,sim.size) for (i in 1:sim.size) { n.step <- nk for (j in 1:k) { pj <- rbeta(1,A[j]+s[j],B[j]+r[j]) p0[i] <- p0[i]*pj n.shortfall <- n.step-s[j] n.step <- s[j]+r[j]+ sum(1+rgeom(n.shortfall,pj)) } n0[i] <- n.step } mk <- (s+r)[k] m0 <- s[1] pred <- quantile(n0,probs=c(0.025,0.5,0.975)) layout(c(1,2,2,2)) par(mar=c(0.1,4.1,0.1,0.1)) pnr.hist <- cut(n0,seq(0,n0.max,length=40)) barplot(table(pnr.hist),horiz=FALSE,axes=F,xlab=" ",ylab=" ", space=0,col="white",names.arg=rep(" ",39)) par(mar=c(4.1,4.1,0.1,0.1)) par(las=2) plot(0,0,type="n",axes=F, xlim=c(0,n0.max),ylim=c(0,nk), xlab="Number needed to recruit", ylab="Number enrolled") axis(side=1) axis(side=2) box() polygon(x=c(mk,pred[1],pred[3]),y=c(m0,nk,nk), density=-1,border=NA,col="gray") segments(0,0,mk,m0) segments(mk,m0,pred[2],nk, col="white") text(pred,nk,round(pred),srt=90,adj=1) text(0,m0,m0) text(0,nk,nk) CrI <- matrix(NA,nrow=k+1,ncol=2) for (j in 1:k) { CrI[j,] <- qbeta(c(0.025,0.975),A[j]+s[j],B[j]+r[j]) text(n0.max,nk*(k+1-j)*0.05, paste("95%CrI for Stage ",j," (", round(CrI[j,1],2),",", round(CrI[j,2],2),")", sep=""),adj=1) } CrI[k+1,] <- quantile(p0,probs=c(0.025,0.975)) text(n0.max,0, paste("95%CrI all stages (", round(CrI[k+1,1],2),",", round(CrI[k+1,2],2),")", sep=""),adj=1) list(n0=n0,p0=p0,CrI=CrI) } A <- c(10,45,25) B <- c(40, 5,25) s00 <- rep(0,3) r00 <- rep(0,3) s07 <- c( 18, 79, 93) r07 <- c( 61, 14, 222) s14 <- c( 93, 433, 499) r14 <- c( 340, 66,1070) prior.results <- projected.number.to.recruit(414,A,B,s00,r00,n0.max=15000) day07.results <- projected.number.to.recruit(414,A,B,s07,r07,n0.max=15000) day14.results <- projected.number.to.recruit(414,A,B,s14,r14,n0.max=15000)
The next logical step is to combine and exponential accrual model with a geometric model of rejection/refusal rates.
You can find an earlier version of this page on my original website.