The rule of 16 is a convenient rule to give quick estimate of the sample size that you might need in a study. It states that if you want to conduct a study with enough power to compare two groups, the number of patients you would need in each group is around 16 divided by the effect size squared.
The rule of 16 was derived by Gerard Van Belle and published in his book, Statistical Rules of Thumb. A draft chapter from his book that discusses the rule of 16 is available on the web.
I wrote a review of this book for the Journal of Biopharmaceutical Statistics, which is also available on the web.
While the rule of 16 should not be used in a formal research paper or in a grant proposal, it is still helpful during the early planning phases of a research study when you are trying to get a rough idea of whether you have a large enough budget to test a particular hypothesis.
Let’s see a few examples of how the rule of 16 might work in a real world setting.
A study in Russia examined physical activity, spinal problems, and quality of life in older adults. This is an observational study and you want to use information from the study to estimate sample sizes for a prospective randomized trial that you plan in the United States.
Ideally, you’d prefer to base your sample size calculations on a study done locally, but let’s assume that this is the only paper you can find and you have to do a bit of an extrapolation.
Extrapolations are often common in sample size justifications. Any study that you might plan is going to be different from previously studied research. Otherwise, why would you do the study? You just have to make a good faith effort to find a study that is reasonably similar, knowing that there will always be some differences.
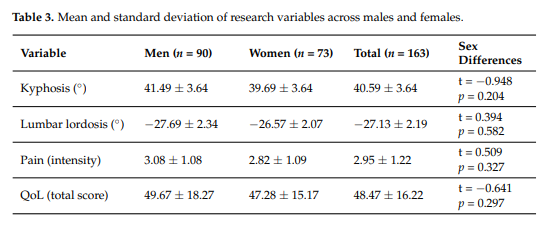
In this study, the key statistics you will need are in table 2 and table 3.
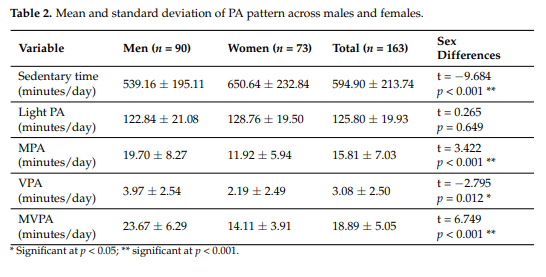
The first outcome variable you will measure is moderate physical activity (MPA). This is measured in minutes. The mean and standard deviations are given for men, women, and combined. Your study will be a mix of men and women, so use the mean (15.81) and the standard deviation (7.03) from the combined column.
After discussion with the research team, you all agree that a 5 minute change in moderate physical activity between the treatment and control groups would be clinically important. This translates to an effect size of
$5 / 7 \approx 0.7$
You can round liberally here because this is just a quick “back of the envelope” calculation.
The rule of 16 says, you would need roughly
$16/0.7^2=16/0.49$
Round again to get
$16/0.5=32$
So for this outcome, you’d need roughly 32 patients per group to detect a 5 minute change in moderate physical activity.
For quality of life (QoL), the researchers used the World Health Organization Quality of Life Scale (WHOQOL-BREF) questionnaire. it was rescaled to range between 0 and 100. The team is divided on this point. Some think that a difference of 10 units is clinically important and other believe that a 15 unit difference is clinically important.
The paper reports a standard deviation of 16 units, so your effect size is
$10/16$ or $5/8$
Apply the rule of 16
$16/(5/8)^2=16/(25/64)=16*64/25$
Thankfully, you have powers of 2 memorized all the way up to 65,536. You know that 16 is 2 raised to the 4th power and 64 is 2 raised to the 6th power, so the product in the numerator is 2 raised to the 10th power or 1,024. Round this to an even thousand. This gives you an approximate sample size of
$1,000/25$ or $40$
So you’d need roughly 40 patients per group to detect a 10 unit shift in quality of life.
The group that thinks that only a 15 unit shift or larger is clinically important gives you an even smaller sample size. The effect size is 15/16 and you might as well round this to 1. The rule of 16 says that you need
$16/1^2=16$
patients per group.
The project has enough in the budget to recruit 100 patients total, or 50 in each group. Your quick sample size calculations (32, 40, and 16) assure you that a formal power calculation using exact formulas rather than approximations will easily demonstrate that 100 patients will provide sufficient power to test reasonable changes in moderate physical activity and quality of life.
Tell the group that you need a day or two to do the formal power calculations, but it looks a total sample size of 100 will work just fine.
Reference:
Victoria Zaborova, Oxana Zolnikova, Natiya Dzhakhaya, Svetlana Prokhorova, Alexander Izotov, Tatyana Butkova, Vasiliy Pustovoyt, Ksenia Yurku, Dmitry Shestakov, Tatyana Zaytseva, and Hassan Shafaei. Associations between Physical Activity and Kyphosis and Lumbar Lordosis Abnormalities, Pain, and Quality of Life in Healthy Older Adults: A Cross-Sectional Study. Healthcare (Basel). 2023-09-29, 11(19), 2651. doi: 10.3390/healthcare11192651. PMID: 37830688; PMCID: PMC10572639.