I received an interesting email recently. Someone was studying the relationship between firearm suicides and veterans to answer the question: “Are veterans more likely to commit suicide with a firearm than non-veterans?”
The data was arranged in a table that looked something like this (I changed the numbers to simplify the calculations)

Then this person proceeded to find seven different formulas for the odds ratio and tried all of them. How I wish more people were this adventurous! Here are the results.
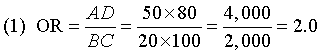
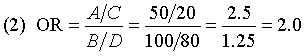
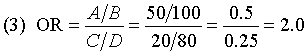
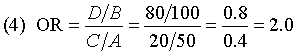
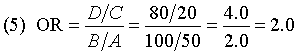
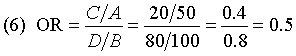
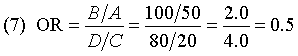
Actually, there may be a couple more formulas, but this is still an amazing list. So how come some of the formulas produce an odds ratio of 2 and some of them produce an odds ratio of 0.5? Is there are rule about how to layout a 2 by 2 table? What are the rows? What are the columns? What order do the rows and columns go in?
The odds ratio is literally a ratio of odds. But there is more than one way to compute the odds and more than one way to compute the ratio.
The first formula is simply a cross-product ratio. It is simple and fast, but does not have a good intuitive explanation.
The second formula computes the odds of a firearm suicide versus non-firearm suicide in vets (2.5 odds or 5 to 2 in favor of a firearm suicide) and compares it to the odds of a firearm suicide versus non-firearm suicide in non-vets (1.25 odds or 5 to 4 in favor of a firearm suicide). This produce a ratio of odds of 2.0.
The third formula computes the odds that a firearm suicide is a veteran versus non-veteran (0.5 odds or 2 to 1 against veterans) and compares it to the odds that a non-firearm suicide is a veteran versus non-veteran (0.25 odds or 4 to 1 against veterans).
The fourth formula computes the odds that odds that a non-veteran is a non-firearm suicide (0.8 odds or 5 to 4 against a non-firearm suicide) and compares it to the odds that a veteran is a non-firearm suicide (0.4 odds or 5 to 2 against a non-firearm suicide).
Now wait, isn’t that backwards? Why would anyone compute an odds ratio this way? It turns out that this is a perfectly fine way to compute an odds ratio, but it sounds awkward because of the lengthy terms non-firearms suicide and non-veteran. If we substitute different words (I realize these words are not quite accurate), the statement would appear perfectly reasonable. So this formula compute the odds of a passive suicide among civilians compared to the odds of a passive suicide among non-civilians.
So why do the formulas (6) and (7) produce different results? Notice that formula (6) is identical to formula (2) except that A and C are swapped and B and D are swapped. You could get this effect if you switched the first and second rows of your table.
The order of your table is arbitrary. You listed the rows in alphabetical order, but there is nothing stopping you from listing the rows in reverse alphabetical order. And since there is more than one way to label the rows, you could still get a different order even if you rigorously enforced alphabetical ordering. The labels “passive suicide” and “violent suicide” have a different alphabetical order than “firearm suicide” and “non-firearm suicide”.
The reason that switching the two rows changes the odds ratio is that you are effectively swapping the numerator and denominator of the odds ratio. And an estimate that was 2.0 becomes 0.5. It is not a coincidence that these two numbers are reciprocals.
So what one estimate is telling you is that being a veteran increases your odds of being a firearm suicide. The odds are twice as high in the veteran group than the non-veteran group. The other odds ratio is telling you that being a non-veteran decreases your odds of being a firearm suicide. The odds in the non-veteran group is about half of the odds in the veteran group.
So your numbers are perfectly consistent, even though they look wildly inconsistent.
So which odds ratio do you use? It’s “dealer’s choice” and no one will complain about any of these choices. Certain groups, such as the Cochran collaboration have set up rules. In the Cochran collaboration, they always orient their tables so that an odds ratio less than one represents benefit for the new therapy versus the standard therapy. But you do not have to follow their convention.
I have some informal rules about how to orient a 2 by 2 table, but these rules are based on making the table easier to comprehend rather than on any rigorous criteria or mathematical formula.
So the good news is that you can do whatever you like. If you do a lot of work with odds ratios (and other ratios like the relative risk), you just have to get comfortable with the fact that an odds ratio of 2.0 and an odds ratio of 0.5 are just the opposite sides of the same coin.
You can find an earlier version of this page on my old website.