Dear Professor Mean, I have a data set that is accumulating more information over time. When I estimate the standard deviation for one of the outcomes in this data set, shouldn’t that value decrease as the sample size increases?
This is a common misconception. The standard deviation does not decline as the sample size increases. The standard error does. One way to think about it is that the standard deviation is a measure of the variability of a single item, while the standard error is a measure of the variability of the average of all the items in the sample.
What does happen is that the estimate of the standard deviation becomes more stable as the sample size increases. But after about 30-50 observations, the instability of the standard deviation becomes negligible.
Here’s an example of a standard deviation calculation on 500 consecutively collected data values. I computed the standard deviation for n=2, 3, 4, …, 200. The standard deviation does wiggle around a bit, especially at sample sizes less than 100. After a while there is no obvious upward or downward trend.
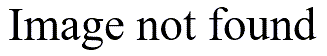
Here is the R code that produced this data and graph.
x <- rnorm(500) s <- rep(NA,500) for (i in 2:500) { s <- sqrt(var(x[1:i])) } par(mar=c(2.1,2.1,1.1,0.1)) plot(s,xlab=" ",ylab=" ")
Related web pages: