There are three steps in a typical survival analysis.
Know how much data you have
Graph the survival function
Compare the survival times
Know how much data you have
How much data do you have. There are several ways of measuring this. The simplest is to note the number of patients that you have studied.
SPSS supplies a data set, AML Survival, that has data on 23 patients, 11 who received chemotherapy and 12 who did not.
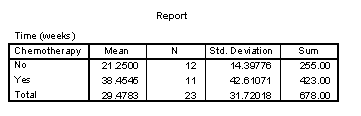
You should also note how long these patients were studied. From the table above, you can see that we had a total of 678 patients weeks of observation, with an average of 32 weeks per patient. There was a greater amount of time observed in the chemotherapy group, 423 patients, or an average of 38 weeks per patient.
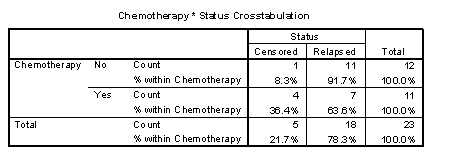
Finally, you should note the number of events that occurred. In this data set, relapse is the event, and we had a total of 18 relapses.
For the most part, it is the number of events, rather than the number of patients or the amount of time followed that determines the precision of your survival data model. You want to see roughly 25 to 50 events per group in order to have a good level of precision. By that standard, this data set is small.
Graph the survival function
The Kaplan Meier survival curve gives you a good estimate of the survival probabilities for each group you are studying.
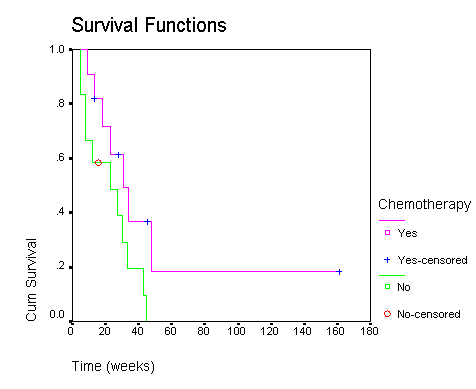
In this graph, the relapse rate appears worse in the no chemotherapy group. Keep in mind, though, that there is a lot of variability in these curves, because the sample size is so small.
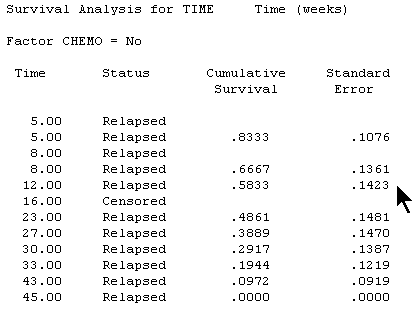
Notice that in the group without chemotherapy, the standard error is 0.14 at 12 weeks. This means that an approximate 95% confidence interval for the 12 week relapse rate would be 0.30 to 0.86.
Compare the survival times
A quick and simple comparison of the survival curves would use the mean, median, and/or quartiles. You could also estimate the survival at a certain time point.
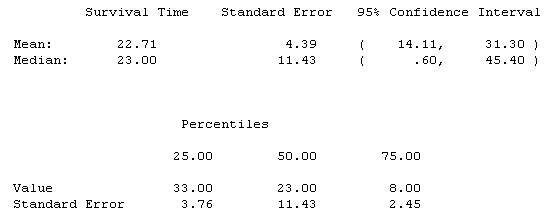
The table above shows the mean, median, and quartiles for the no chemotherapy group. The median relapse time is 23 weeks, but the confidence interval extends all the way from 0.6 to 45.4 weeks.
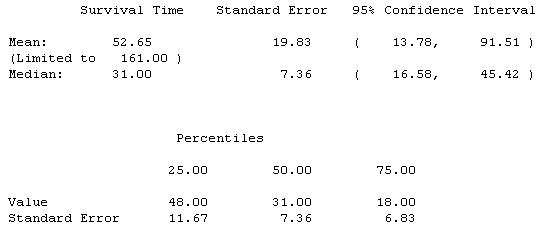
The median survival time for the group with chemotherapy is larger, 31 weeks, but again there is a lot of variability in this estimate.
Sometimes you cannot estimate the median survival time, particularly if the number of events in the group is much less than half of the patients studied.
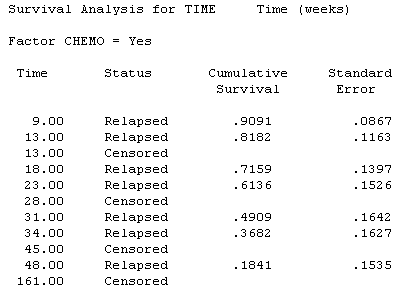
Suppose we are interested in the probability of relapse within half a year (26 weeks). There is no data at 26 weeks, so you round down to the nearest value. For the group with chemotherapy, the table directly above shows the estimated relapse rate at 23 weeks to be 0.61 with a standard error of 0.15. For the group without chemotherapy the estimated relapse rate at 0.49 with a standard error of 0.15. So the group with chemotherapy appears to have better values, but this difference is dwarfed by the uncertainty in the data.
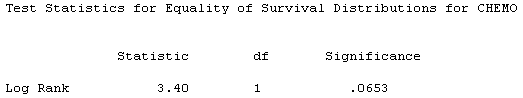
The simplest formal test that compares two survival curves is the log rank test. In this example, the p-value is borderline, indicating a possible trend, but not quite achieving statistical significance.
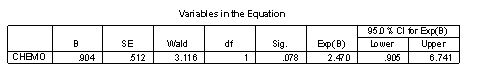
The Cox regression model is more complex, but it can look at relationships with both continuous and categorical predictors. This model estimates a hazard ratio of 2.5, with confidence limits going from 0.9 to 6.7. The hazard ratio could be interpreted as a relative risk. The risk of relapse is 2.5 times greater in the group without chemotherapy. Although this ratio is large, it does not quite achieve statistical significance due to the small sample size.
You can find an earlier version of this page on my original website.