When I run, I have an app that announces the distance traveled (in kilometers) at the end of every minute. But since the app rounds to one decimal place, there is a bit of uncertainty in the pace that I might compute. Here’s how I would address this uncertainty using a Taylor series approximation.
Pace is the inverse of speed. You divide the time in minutes by the distance traveled. The math is usually pretty easy. It is a simple division of two numbers both of which (for my runs) are in the double digits.
Simple example of the linear Taylor series approximation
For example, suppose my GPS told me that I had just finished 2.5 kilometers in 20 minutes. I’m actually slower than that, but I used to run at that pace. The pace is
\(\frac{20}{2.5}=8\) minutes per kilometer.
My app rounds distance to one decimal, so that denominator of 2.5 might be as small as 2.45 or as large as 2.55. I could compute the two ratios,
\(\frac{20}{2.45}=8.1633\) and
\(\frac{20}{2.55}=7.8431\)
but dividing by a three digit number is tricky. I don’t carry a calculator and I don’t have the opportunity to write out the calculation on a pad of paper.
Taylor series approximation to the rescue! The linear Taylor series approximation is
\(f(x) \approx f(a)+(x-a)f'(a)\)
This approximation is pretty good in most cases. You have to have the value of a be not too far from the value of x. You also need the function f to be reasonably well behaved. This means no extreme fluctuations and no sudden transitions in shape.
This is certainly the case for the function
\(f(x)=\frac{20}{x}\)
The derivative is
\(f'(x)=-\frac{20}{x^2}\)
So the linear Taylor series approximation is
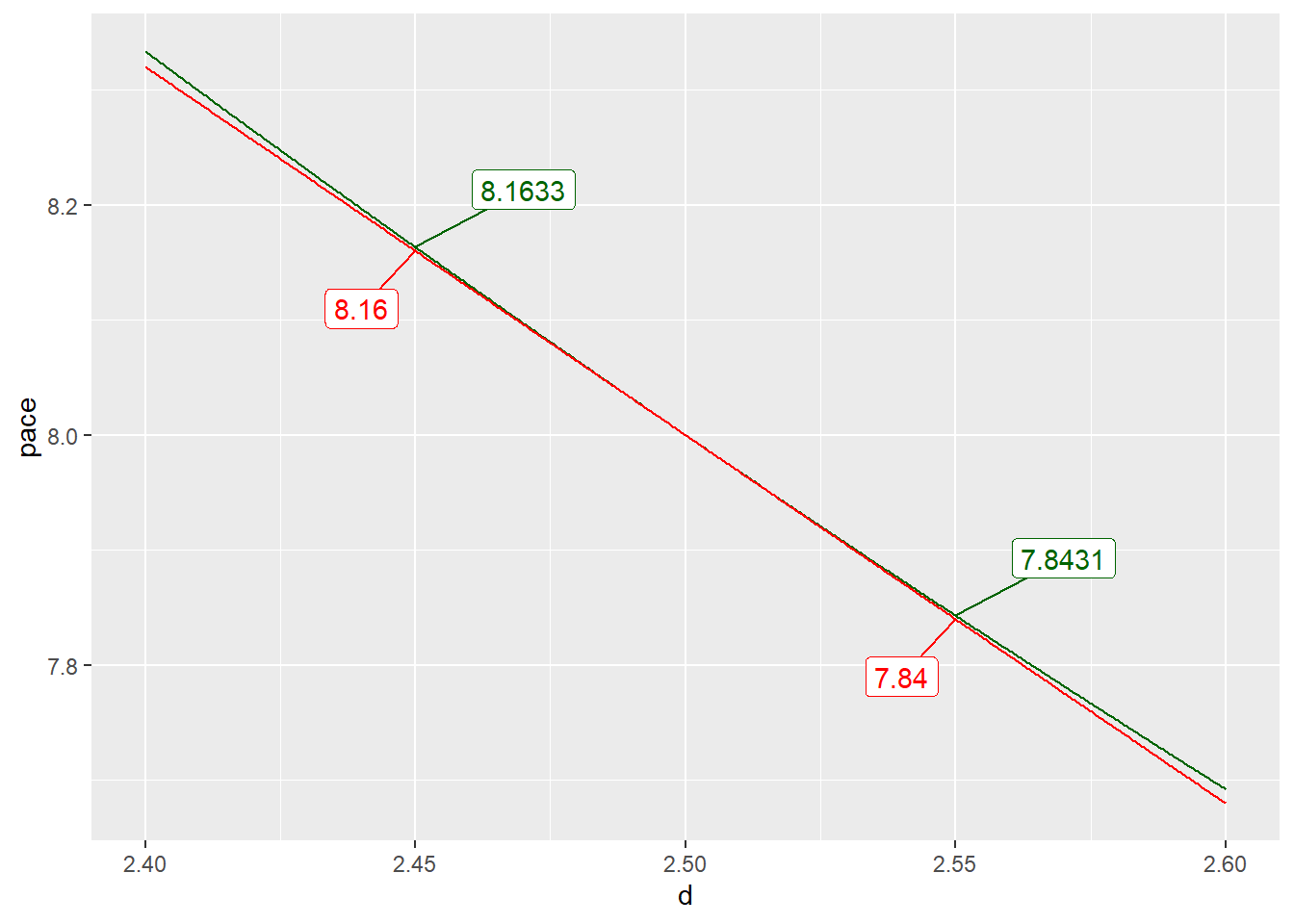
\(f(2.45) \approx \frac{20}{2.5}-(2.45-2.5)\frac{20}{2.5^2}=8.16\) and
\(f(2.55) \approx \frac{20}{2.5}-(2.55-2.5)\frac{20}{2.5^2}=7.84\) minutes per kilometer
Notice that you do divide by nice round numbers like 2.5 and \(2.5^2\) rather than 2.45 and 2.55.
Graphical illustation of the linear Taylor series approximation
Here’s a graphical illustration of the linear Taylor series approximation. The green line represents pace as it actually should be calculated and the red line represents the linear Taylor series approximation.
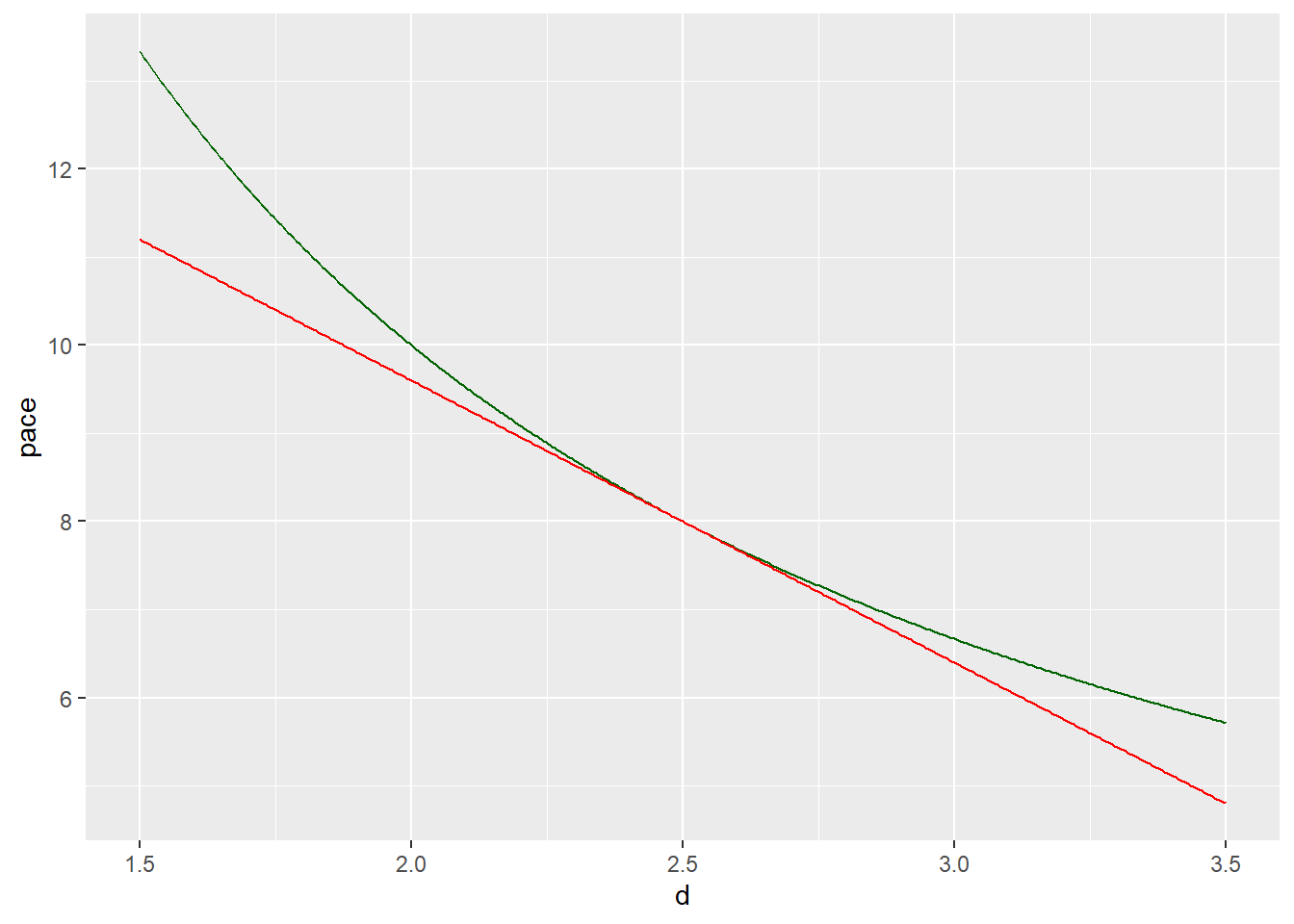
The approximation is good when the distance is close to 2.5 kilometers, but does poorly further away. Fortunately, we are interested in this approximation at 2.45 and 2.55.
Let’s zoom in.
General application of the linear Taylor series approximation
Let’s look at a more general case. You run a total of d kilometers in time t, but because of rounding, d could be a bit smaller (d-0.05) or a bit larger (d+0.05). Treating t as constant, define
\(f(d)=\frac{t}{d}\)
Then, the linear Taylor series approximation is
\(f(d + 0.05) \approx \frac{t}{d} - 0.05\frac{t}{d^2}\) and
\(f(d - 0.05) \approx \frac{t}{d} + 0.05\frac{t}{d^2}\).
You can factor this to
\(f(d + 0.05) \approx \frac{t}{d}\Big(1 - \frac{0.05}{d}\Big)\) and
\(f(d - 0.05) \approx \frac{t}{d}\Big(1 + \frac{0.05}{d}\Big)\)
So after running 2.5 kilometers, the rounding error causes an inaccuracy in the pace calculation by about 0.05 / 2.5 or 2% in either direction. After running 5 kilometers, the rounding error causes an inaccuracy of no more than 0.05 / 5 or 1% in either direction. Notice that the signs flip. If you run slightly less than 2.5 kilometers, your pace is higher (slower). If you run slightly more than 2.5 kilometers, your pace is lower (faster).
You can state things in an even greater degree of generality. The rounding error in distance (as a percentage) translates directly to the rounding error in pace. This is an approximation, but it turns out to be a pretty good approximation as long as the percentage rounding error is small.