I am giving a talk today for the Kansas City R Users group about BUGS (Bayes Using Gibbs Sampler). I have already written extensively about BUGS and the interface to BUGS from within the R programming environment
- and you can find these on my category page for Bayesian statistics. Here is a quick overview of why you might want to use BUGS and how you would use it. I’ve included links to the relevant pages on my website so you can explore this topic further on your own.
First
- you need to remember the basics of Bayesian statistics. Bayesian statistics takes a different philosophical approach than traditional hypothesis testing. It views the parameters of a hypothesis as random variables. These random variables are described using a prior distribution. You collect some data and examine the likelihood of the data given the prior distribution. Using Bayes Theorem
- you combine the prior distribution and the likelihood to get a posterior distribution.
Here’s a simple practical example. You are running a randomized clinical trial that needs to recruit 350 patients. You’re not sure how long it will take to recruit this many patients. You’re thinking it will take three years to recruit that many patients. This implies that you will be able to find a new patient every 3.1 days on average. There is substantial uncertainty about this estimate
- though and we characterize the waiting time distribution using an inverse gamma distribution with parameters k=175 and V=182.5. Here’s what that distribution looks like:
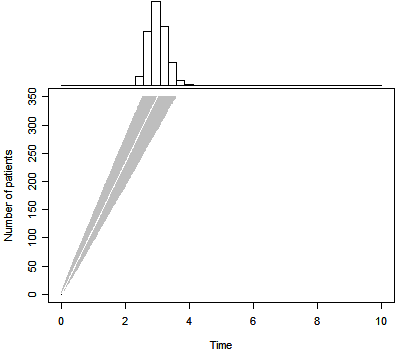
Now
- you start running your clinical trial
- and you notice that things are going slower than planned. After 239 days
- you’ve recruited only 41 subjects. The average waiting time is 239 /41 = 5.8 days per patient. What is your expected completion time now?
You combine your prior beliefs with the existing data to get a posterior distribution of the waiting time
- which turns out to be a weighted average of the observed accrual data and your prior beliefs. This leads to an updated prediction of the completion time for the clinical trial.
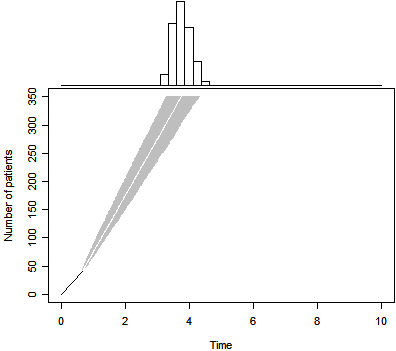
This use of prior distributions is extremely controversial
- because it incorporates subjective opinions into the data analysis process. Often a Bayesian data analyst will choose a diffuse or non-informative prior distribution. This represents a prior distribution that is spread so thinly across the possible parameters that it does not influence the posterior distribution. Here’s what such a distribution would produce in the patient accrual example.
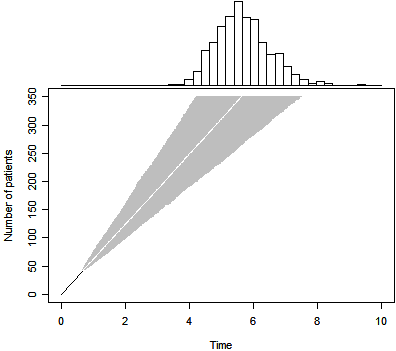
Notice that this represents a simple linear extrapolation of the waiting times. These graphs come from a webpage I wrote a while back.
The mathematics of Bayesian data analysis is quite complex. Here’s a description on the Wikipedia page on posterior distributions.
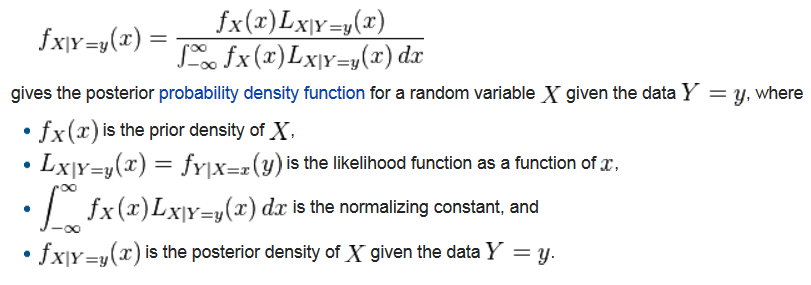
The denominator
- the normalizing constant
- is a killer. Often the integral is impossible to compute. It is often difficult to come up with a numerical estimate. You might recall the trapezoidal rule and Simpson’s rule from Calculus
- but this integral is often mutli-dimensional
- making these approaches impractical.
Back in the early 1990s statisticians discovered a new computer simulation approach that avoids the complexities of the normalizing constant. It was actually a rediscovery of methods developed much earlier
- but which were largely unknown in the Statistics community. This approach
- which goes under a variety of names
- such as the Metropolis algorithm
- the Gibbs sampler
- and Markov Chain Monte Carlo requires only that you can specify the numerator of the equation above. It uses an acceptance/rejection approach where the estimate of the posterior distribution either stays at its current location or jumps to a different location. I have a nice example of how this works in a very simple unidimensional case
- but this process works very efficiently even in the multidimensional case.
The simulation approach has two issues that you must account for at all times. First
- the consecutive values in the simulation are positively correlated to a more than trivial amount. If you don’t get a huge number of simulations
- the results will look “patchy” and will be a poor representation of the posterior distribution. Often you will need thousands or tens of thousands of values.
Second
- the simulation has to be given a starting value and it has to be given time to converge. You will often need to run the simulation a thousand times or more before the results become reliable. Diagnosing convergence is tricky. One possibility is to run the same problem with two different starting points and see when the two distributions mix properly.
 {width=“405”
height=“437”}
{width=“405”
height=“437”}
This example from a webpage discussing segmented linear regression models shows that it is naive to expect convergence after a thousand simulations and that perhaps as many as 3,000 simulations should be run before convergence.
The software to run these simulations was developed by a group headed by David Spiegelhalter. Their program
- WinBUGS
- is with a difficult syntax (which is an unavoidable manifestation of the complexity of the simulation models) and a menu driven interface. WinBUGS
- as the name implies
- is Windows specific. A newer version
- OpenBUGS
- was written to run under a wider range of operating systems. OpenBUGS was written in the Component Pascal programming language
- and that choice has led to other difficulties with portability
- so a new program
- JAGS
- was developed in C++.
The acronym BUGS stands for Bayes Using Gibbs Sampler and the acronym JAGS stands for Just Another Gibbs Sampler.
If you want to run WinBUGS
- OpenBUGS
- or JAGS
- you should do it within R
- as it bypasses the tedious menu driven interface and it allows you to use all the data management capabilities within R. There are a variety of interfaces
- but you need to be aware of issues associated with the Windows specific operating systems
- including the use of 32 bit versus 64 bit Windows. I wrote up a webpage covering some of these complexities.
I have recently been using JAGS and the R interface to JAGS (rjags). It seems to have fewer compatibility issues and the error messages are a bit less cryptic. Here’s an example of how to run JAGS from within R.
Why would you want to learn Bayesian data analysis software? Bayesian data analysis is moderately complex
- but it turns out that this level of complexity does not get worse as the problems themselves get more complex. This is in contrast to classical methods that are easy for easy problems, but which escalate rapidly into the incomprehensible.
Bayesian methods are especially useful for multi-level models (also known as mixed models), which are difficult to the point of being almost intractactable using classical methods.
You can find an earlier version of this page on my blog.