Wikipedia entry on Binomial Confidence Interval, Part 2

[StATS]: Wikipedia entry on Binomial Confidence Interval, Part 2 (August 22, 2006). Category: Wiki pages

Here’s my first attempt to improve the Wikipedia entry on the binomial confidence interval. I start by simplifying and improving the introduction

A ‘‘‘Binomial Confidence Interval’’’ is a [confidence interval] for a proportion in a [statistical population]. It uses the proportion estimated in a [statistical sample] and allows for [sampling error]. There are several formulas for a binomial confidence interval, but all of them rely on the assumption of a [binomial distribution]. A simple example of a [binomial distribution] is the number of heads that you observe when you flip a coin in the ten times. In general, a [binomial distribution] applies when you repeat an experiment a fixed number of times, each trial of the experiment has two possible outcomes (labeled arbitrarily success and failure), the probability of success is the same for each trial, and the trials are [statistically independent].

and including the classical formula that relies on a normal approximation.

The simplest and most commonly used formula for a binomial confidence interval relies on approximating the [binomial distribution] with a [normal distribution]. This approximation is justified by the [central limit theorem]. The formula is

$\backslash hat\; p\; \backslash pm\; z\_\{\backslash alpha\; /2\}$ $\backslash sqrt\{\; \backslash frac\{\backslash hat\; p\; \backslash left\; (\; 1-\; \backslash hat\; p\; \backslash right\; )\}\{n\}\}$

where $\backslash hat\; p$ is the proportion estimated from the statistical sample, $z\_\{\backslash alpha\; /2\}$ is the $\backslash alpha\; /2$ upper percentile of a [standard normal distribution], and n is the sample size.

The [central limit theorem] applies well to a [binomial distribution], even with a sample size less than 30, as long as the proportion is not too close to 0 or 1. For very extreme probabilities, though, a sample size of 30 or more may still be inadequate. The normal approximation fails totally when the sample proportion is exactly zero or exactly one. A frequently cited rule of thumb is that the normal approximation works well as long as np>5 and n(1-p)>5.

Here’s a screen shot of my changes

and

I also experimented with some messier formulas. Here is the TeX code

$\backslash sum\_\{k=x\}^n\; \{\{n\; \backslash choose\; k\}p\_0^k\; \backslash left\; (\; 1-p\_0\; \backslash right\; )\; ^\; \{n-k\}\; \}=\backslash alpha\; /2$

$\backslash sum\_\{k=0\}^x\; \{\{n\; \backslash choose\; k\}p\_0^k\; \backslash left\; (\; 1-p\_0\; \backslash right\; )\; ^\; \{n-k\}\; \}=\backslash alpha\; /2$

and here is what the equations look like

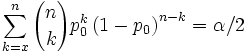
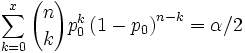
There is no entry for standard normal distribution, and the entry on statistical sample

• en.wikipedia.org/wiki/Statistical_sample

is flagged by Wikpedia as a stub (an entry that is short and provides insufficient information). So it looks like there would be plenty of work for me if I wanted to do more with Wikipedia.

This work is licensed under a Creative Commons Attribution 3.0 United States License. It was written by Steve Simon and was last modified on 04/01/2010.

This page was written by Steve Simon while working at Children’s Mercy Hospital. Although I do not hold the copyright for this material, I am reproducing it here as a service, as it is no longer available on the Children’s Mercy Hospital website. Need more information? I have a page with general help resources. You can also browse for pages similar to this one at

for pages similar to this one at with general help resources. You can also browse Children’s Mercy Hospital website. Need more information? I have a page reproducing it here as a service, as it is no longer available on the Hospital. Although I do not hold the copyright for this material, I am This page was written by Steve Simon while working at Children’s Mercy